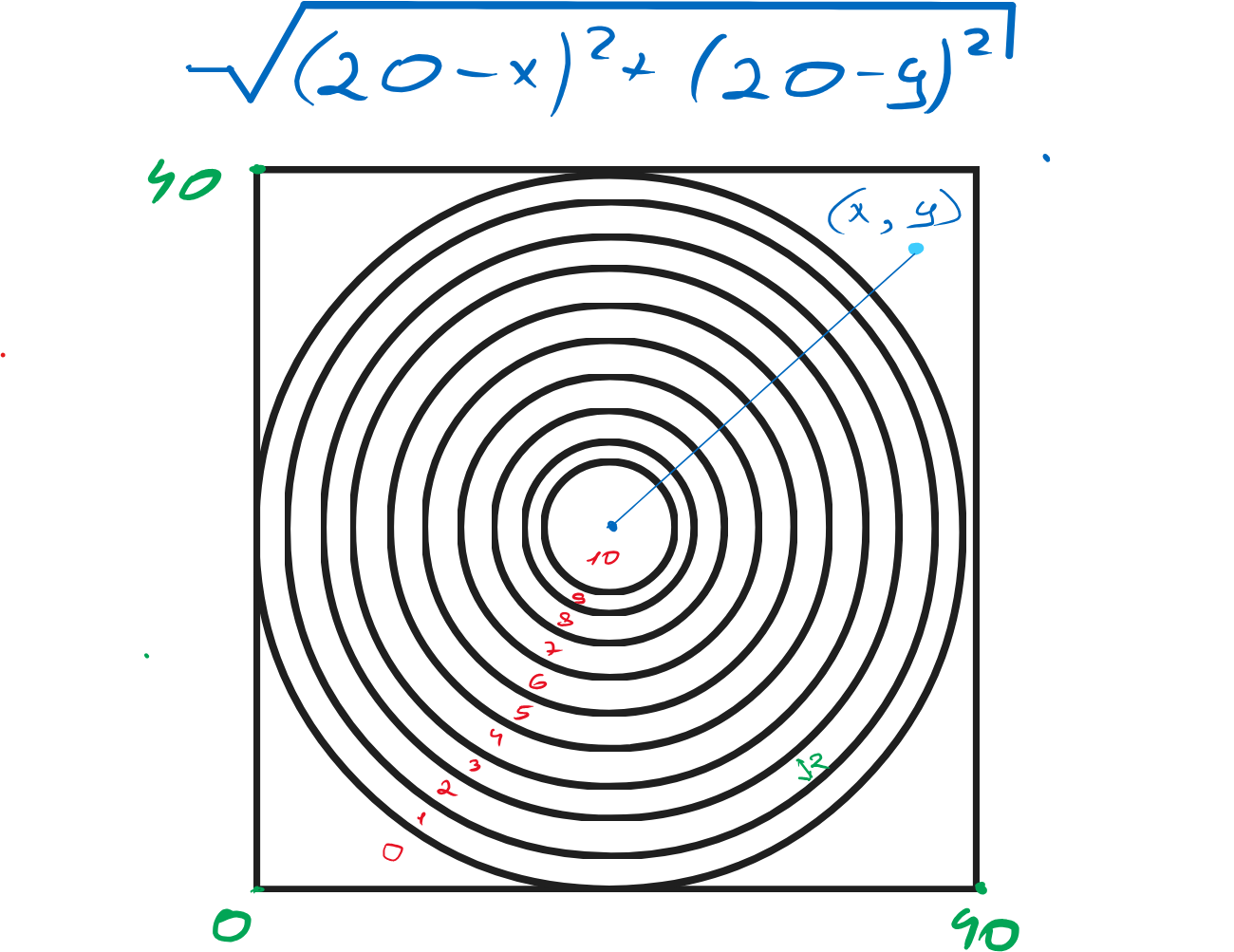
Badanie dotyczy symulacji strzałów łucznika do tarczy o wymiarach 40 x 40 cm. Model symulacyjny generuje losowe współrzędne (X, Y) dla strzałów, a każdy strzał zdobywa różną ilość punktów w zależności od miejsca trafienia. Tarcza ma współśrodkowe pierścienie punktacyjne oraz centralne koło.
W pierwszej części symulacji przeprowadzono strzały w trzech próbach: 10, 100 i 1000 razy. Obliczono średnie wyniki i odchylenia standardowe dla każdej próby, co pozwoliło ocenić skuteczność strzałów. Następnie sprawdzono, czy średni wynik jest istotnie większy od 5 punktów oraz stworzono histogramy obrazujące rozkład punktów.
Ostateczne wnioski pomogą ocenić skuteczność modelu symulacyjnego oraz zrozumieć, jak wyniki strzałów rozkładają się na tarczy.
import random
import numpy as np
import math
from scipy import stats
import matplotlib.pyplot as plt
# Parametry
n = 10
x_c = []
y_c = []
res_xy = []
point_xy = []
# Generowanie danych
for i in range(n):
x_c.append(random.uniform(0, 40))
y_c.append(random.uniform(0, 40))
res_xy.append(math.sqrt(math.pow(20 - x_c[i], 2) + math.pow(20 - y_c[i], 2)))
# Ustalanie punktów na podstawie odległości
if 20 < res_xy[i]:
point_xy.append(0)
elif 18 < res_xy[i] < 20:
point_xy.append(1)
elif 16 < res_xy[i] < 18:
point_xy.append(2)
elif 14 < res_xy[i] < 16:
point_xy.append(3)
elif 12 < res_xy[i] < 14:
point_xy.append(4)
elif 10 < res_xy[i] < 12:
point_xy.append(5)
elif 8 < res_xy[i] < 10:
point_xy.append(6)
elif 6 < res_xy[i] < 8:
point_xy.append(7)
elif 4 < res_xy[i] < 6:
point_xy.append(8)
elif 2 < res_xy[i] < 4:
point_xy.append(9)
elif 0 < res_xy[i] < 2:
point_xy.append(10)
# Testowanie hipotezy o średniej
t_statistic, p_value = stats.ttest_1samp(point_xy, 5)
print(f"Wartość t: {t_statistic}")
print(f"Wartość p: {p_value}")
if p_value < 0.05 and t_statistic > 0:
print("Średnia jest statystycznie istotnie większa od 5.")
else:
print("Brak statystycznej istotności w odniesieniu do 5.")
# Statystyki
print(point_xy)
print(f"Średnia: {np.average(point_xy)}")
print(f"Odchylenie standardowe: {np.std(point_xy)}")
# d) Rysowanie histogramu
plt.hist(point_xy, bins=np.arange(-0.5, 11.5, 1), density=True, alpha=0.7, color='blue')
plt.title('Histogram wyników łucznika')
plt.xlabel('Wyniki')
plt.ylabel('Gęstość')
plt.xticks(range(11))
plt.grid(True)
plt.show()
# e) Weryfikacja rozkładu równomiernego
observed_counts = np.bincount(point_xy, minlength=11)
# Oblicz oczekiwane wartości
expected_counts = np.full(11, n / 11)
# Sprawdzamy sumy
print(f"Obserwowane częstotliwości: {observed_counts}")
print(f"Oczekiwane częstotliwości: {expected_counts}")
# Test Chi-kwadrat
chi2_statistic, p_value_chi2 = stats.chisquare(observed_counts, expected_counts)
print(f"Wartość Chi-kwadrat: {chi2_statistic}")
print(f"Wartość p (test Chi-kwadrat): {p_value_chi2}")
if p_value_chi2 < 0.05:
print("Odrzucamy hipotezę o rozkładzie równomiernym.")
else:
print("Nie ma podstaw do odrzucenia hipotezy o rozkładzie równomiernym.")Wartość t: -2.3333333333333335
Wartość p: 0.044503537305576386
Brak statystycznej istotności w odniesieniu do 5.
[4, 4, 0, 1, 7, 5, 1, 7, 0, 0]
Średnia: 2.9
Odchylenie standardowe: 2.6999999999999997

Obserwowane częstotliwości: [3 2 0 0 2 1 0 2 0 0 0]
Oczekiwane częstotliwości: [0.90909091 0.90909091 0.90909091 0.90909091 0.90909091 0.90909091
0.90909091 0.90909091 0.90909091 0.90909091 0.90909091]
Wartość Chi-kwadrat: 14.199999999999996
Wartość p (test Chi-kwadrat): 0.1640629037577191
Nie ma podstaw do odrzucenia hipotezy o rozkładzie równomiernym.
import random
import numpy as np
import math
from scipy import stats
import matplotlib.pyplot as plt
# Parametry
n = 100
x_c = []
y_c = []
res_xy = []
point_xy = []
# Generowanie danych
for i in range(n):
x_c.append(random.uniform(0, 40))
y_c.append(random.uniform(0, 40))
res_xy.append(math.sqrt(math.pow(20 - x_c[i], 2) + math.pow(20 - y_c[i], 2)))
# Ustalanie punktów na podstawie odległości
if 20 < res_xy[i]:
point_xy.append(0)
elif 18 < res_xy[i] < 20:
point_xy.append(1)
elif 16 < res_xy[i] < 18:
point_xy.append(2)
elif 14 < res_xy[i] < 16:
point_xy.append(3)
elif 12 < res_xy[i] < 14:
point_xy.append(4)
elif 10 < res_xy[i] < 12:
point_xy.append(5)
elif 8 < res_xy[i] < 10:
point_xy.append(6)
elif 6 < res_xy[i] < 8:
point_xy.append(7)
elif 4 < res_xy[i] < 6:
point_xy.append(8)
elif 2 < res_xy[i] < 4:
point_xy.append(9)
elif 0 < res_xy[i] < 2:
point_xy.append(10)
# Testowanie hipotezy o średniej
t_statistic, p_value = stats.ttest_1samp(point_xy, 5)
print(f"Wartość t: {t_statistic}")
print(f"Wartość p: {p_value}")
if p_value < 0.05 and t_statistic > 0:
print("Średnia jest statystycznie istotnie większa od 5.")
else:
print("Brak statystycznej istotności w odniesieniu do 5.")
# Statystyki
print(point_xy)
print(f"Średnia: {np.average(point_xy)}")
print(f"Odchylenie standardowe: {np.std(point_xy)}")
# d) Rysowanie histogramu
plt.hist(point_xy, bins=np.arange(-0.5, 11.5, 1), density=True, alpha=0.7, color='blue')
plt.title('Histogram wyników łucznika')
plt.xlabel('Wyniki')
plt.ylabel('Gęstość')
plt.xticks(range(11))
plt.grid(True)
plt.show()
# e) Weryfikacja rozkładu równomiernego
observed_counts = np.bincount(point_xy, minlength=11)
# Oblicz oczekiwane wartości
expected_counts = np.full(11, n / 11)
# Sprawdzamy sumy
print(f"Obserwowane częstotliwości: {observed_counts}")
print(f"Oczekiwane częstotliwości: {expected_counts}")
# Test Chi-kwadrat
chi2_statistic, p_value_chi2 = stats.chisquare(observed_counts, expected_counts)
print(f"Wartość Chi-kwadrat: {chi2_statistic}")
print(f"Wartość p (test Chi-kwadrat): {p_value_chi2}")
if p_value_chi2 < 0.05:
print("Odrzucamy hipotezę o rozkładzie równomiernym.")
else:
print("Nie ma podstaw do odrzucenia hipotezy o rozkładzie równomiernym.")Wartość t: -7.97956423071217
Wartość p: 2.654735563787352e-12
Brak statystycznej istotności w odniesieniu do 5.
[0, 1, 1, 4, 2, 2, 0, 7, 0, 0, 2, 8, 0, 5, 5, 2, 2, 7, 0, 9, 0, 3, 1, 0, 3, 0, 1, 6, 0, 0, 0, 1, 1, 6, 2, 3, 4, 0, 1, 2, 0, 5, 2, 2, 4, 0, 0, 7, 2, 4, 2, 8, 1, 0, 4, 1, 6, 1, 9, 2, 8, 0, 0, 4, 2, 1, 4, 3, 1, 1, 2, 2, 5, 5, 7, 4, 2, 5, 4, 1, 0, 7, 1, 3, 4, 7, 0, 2, 8, 1, 4, 0, 8, 1, 2, 0, 5, 4, 8, 9]
Średnia: 2.86
Odchylenie standardowe: 2.6684077649414832
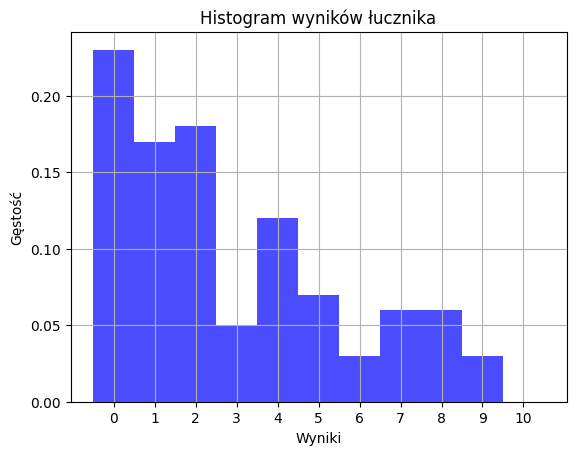
Obserwowane częstotliwości: [23 17 18 5 12 7 3 6 6 3 0]
Oczekiwane częstotliwości: [9.09090909 9.09090909 9.09090909 9.09090909 9.09090909 9.09090909
9.09090909 9.09090909 9.09090909 9.09090909 9.09090909]
Wartość Chi-kwadrat: 59.5
Wartość p (test Chi-kwadrat): 4.505868839531248e-09
Odrzucamy hipotezę o rozkładzie równomiernym.
import random
import numpy as np
import math
from scipy import stats
import matplotlib.pyplot as plt
# Parametry
n = 1000
x_c = []
y_c = []
res_xy = []
point_xy = []
# Generowanie danych
for i in range(n):
x_c.append(random.uniform(0, 40))
y_c.append(random.uniform(0, 40))
res_xy.append(math.sqrt(math.pow(20 - x_c[i], 2) + math.pow(20 - y_c[i], 2)))
# Ustalanie punktów na podstawie odległości
if 20 < res_xy[i]:
point_xy.append(0)
elif 18 < res_xy[i] < 20:
point_xy.append(1)
elif 16 < res_xy[i] < 18:
point_xy.append(2)
elif 14 < res_xy[i] < 16:
point_xy.append(3)
elif 12 < res_xy[i] < 14:
point_xy.append(4)
elif 10 < res_xy[i] < 12:
point_xy.append(5)
elif 8 < res_xy[i] < 10:
point_xy.append(6)
elif 6 < res_xy[i] < 8:
point_xy.append(7)
elif 4 < res_xy[i] < 6:
point_xy.append(8)
elif 2 < res_xy[i] < 4:
point_xy.append(9)
elif 0 < res_xy[i] < 2:
point_xy.append(10)
# Testowanie hipotezy o średniej
t_statistic, p_value = stats.ttest_1samp(point_xy, 5)
print(f"Wartość t: {t_statistic}")
print(f"Wartość p: {p_value}")
if p_value < 0.05 and t_statistic > 0:
print("Średnia jest statystycznie istotnie większa od 5.")
else:
print("Brak statystycznej istotności w odniesieniu do 5.")
# Statystyki
print(point_xy)
print(f"Średnia: {np.average(point_xy)}")
print(f"Odchylenie standardowe: {np.std(point_xy)}")
# d) Rysowanie histogramu
plt.hist(point_xy, bins=np.arange(-0.5, 11.5, 1), density=True, alpha=0.7, color='blue')
plt.title('Histogram wyników łucznika')
plt.xlabel('Wyniki')
plt.ylabel('Gęstość')
plt.xticks(range(11))
plt.grid(True)
plt.show()
# e) Weryfikacja rozkładu równomiernego
observed_counts = np.bincount(point_xy, minlength=11)
# Oblicz oczekiwane wartości
expected_counts = np.full(11, n / 11)
# Sprawdzamy sumy
print(f"Obserwowane częstotliwości: {observed_counts}")
print(f"Oczekiwane częstotliwości: {expected_counts}")
# Test Chi-kwadrat
chi2_statistic, p_value_chi2 = stats.chisquare(observed_counts, expected_counts)
print(f"Wartość Chi-kwadrat: {chi2_statistic}")
print(f"Wartość p (test Chi-kwadrat): {p_value_chi2}")
if p_value_chi2 < 0.05:
print("Odrzucamy hipotezę o rozkładzie równomiernym.")
else:
print("Nie ma podstaw do odrzucenia hipotezy o rozkładzie równomiernym.")Wartość t: -24.477342899039705
Wartość p: 4.916845161743252e-104
Brak statystycznej istotności w odniesieniu do 5.
[0, 3, 0, 1, 5, 2, 5, 6, 3, 2, 3, 1, 7, 2, 0, 2, 6, 2, 2, 6, 4, 5, 6, 2, 6, 0, 4, 4, 0, 1, 0, 0, 1, 2, 4, 4, 0, 0, 2, 0, 8, 5, 2, 1, 3, 5, 8, 6, 9, 2, 8, 3, 2, 3, 3, 3, 3, 2, 3, 1, 5, 2, 0, 2, 6, 0, 3, 2, 2, 5, 1, 0, 3, 8, 0, 7, 4, 1, 7, 9, 2, 3, 7, 3, 2, 0, 5, 3, 1, 5, 5, 0, 2, 3, 1, 4, 4, 3, 3, 1, 3, 2, 1, 1, 2, 1, 8, 1, 6, 5, 6, 4, 7, 0, 2, 1, 0, 0, 0, 3, 2, 2, 7, 3, 0, 4, 5, 2, 0, 1, 3, 2, 6, 5, 7, 0, 0, 8, 1, 0, 8, 1, 0, 0, 3, 4, 2, 3, 0, 1, 0, 0, 2, 8, 4, 2, 5, 0, 3, 2, 1, 6, 5, 5, 4, 1, 0, 1, 0, 3, 0, 3, 4, 1, 5, 5, 4, 5, 4, 4, 3, 5, 2, 2, 10, 1, 3, 0, 0, 7, 0, 2, 5, 8, 2, 2, 1, 7, 2, 0, 2, 1, 2, 3, 6, 4, 2, 3, 2, 6, 4, 1, 5, 4, 8, 4, 6, 4, 3, 1, 2, 6, 0, 2, 1, 2, 0, 1, 2, 1, 1, 1, 1, 4, 8, 3, 0, 1, 6, 0, 1, 0, 5, 0, 3, 0, 5, 1, 4, 6, 2, 0, 7, 2, 2, 0, 3, 1, 2, 4, 8, 3, 8, 6, 3, 0, 6, 3, 5, 0, 1, 5, 0, 0, 0, 7, 5, 3, 2, 6, 7, 1, 0, 8, 3, 1, 3, 0, 0, 0, 8, 2, 0, 6, 2, 5, 6, 8, 4, 9, 3, 5, 2, 4, 0, 2, 1, 10, 0, 6, 1, 1, 5, 6, 8, 0, 8, 1, 5, 2, 6, 3, 4, 5, 5, 2, 1, 1, 2, 4, 6, 3, 0, 4, 5, 0, 7, 6, 5, 6, 1, 2, 4, 4, 1, 7, 3, 0, 4, 0, 6, 6, 0, 1, 0, 1, 1, 2, 1, 8, 7, 1, 2, 0, 3, 5, 2, 6, 1, 2, 3, 2, 1, 1, 3, 5, 1, 5, 7, 3, 3, 0, 5, 3, 1, 0, 0, 3, 3, 8, 5, 4, 0, 2, 1, 1, 4, 9, 0, 6, 4, 6, 2, 5, 3, 4, 0, 4, 4, 9, 4, 2, 1, 4, 6, 1, 3, 4, 2, 2, 3, 0, 0, 4, 3, 6, 0, 7, 1, 3, 2, 0, 5, 0, 7, 9, 6, 0, 4, 0, 3, 5, 6, 1, 0, 2, 7, 2, 2, 1, 7, 5, 1, 9, 0, 8, 5, 1, 0, 9, 0, 3, 5, 0, 1, 7, 1, 4, 0, 9, 2, 2, 7, 2, 6, 0, 0, 1, 0, 7, 0, 1, 0, 6, 0, 5, 7, 2, 0, 3, 0, 4, 3, 3, 1, 0, 3, 9, 4, 4, 3, 3, 2, 6, 8, 0, 2, 5, 1, 3, 4, 4, 0, 5, 1, 2, 0, 1, 3, 0, 2, 4, 0, 7, 8, 9, 0, 0, 3, 0, 1, 7, 3, 2, 4, 4, 0, 2, 4, 0, 3, 1, 0, 2, 5, 4, 1, 0, 5, 0, 4, 0, 7, 1, 1, 3, 9, 1, 7, 0, 4, 6, 5, 5, 9, 0, 4, 6, 0, 0, 8, 0, 0, 6, 4, 5, 5, 2, 5, 2, 1, 0, 2, 0, 2, 2, 1, 3, 0, 5, 3, 6, 5, 8, 4, 7, 0, 0, 4, 1, 1, 3, 1, 2, 1, 2, 0, 2, 5, 5, 1, 1, 6, 1, 6, 3, 2, 8, 7, 2, 0, 3, 6, 4, 1, 2, 5, 3, 5, 0, 2, 2, 0, 1, 7, 2, 2, 4, 5, 0, 2, 0, 0, 9, 2, 9, 0, 10, 8, 4, 0, 1, 0, 2, 2, 6, 6, 0, 3, 5, 6, 3, 1, 0, 4, 6, 3, 1, 1, 0, 0, 1, 0, 0, 5, 1, 10, 4, 3, 4, 1, 7, 2, 0, 10, 5, 3, 4, 4, 2, 6, 1, 0, 2, 2, 2, 1, 6, 8, 3, 0, 3, 5, 3, 2, 5, 4, 3, 4, 8, 5, 2, 4, 2, 3, 0, 8, 2, 4, 0, 0, 3, 0, 4, 2, 2, 3, 0, 8, 7, 2, 1, 1, 0, 7, 3, 5, 0, 0, 8, 0, 2, 2, 6, 7, 2, 1, 4, 0, 1, 4, 0, 1, 0, 10, 7, 5, 0, 2, 1, 0, 1, 7, 7, 4, 1, 0, 3, 1, 0, 2, 7, 6, 2, 0, 0, 0, 0, 0, 2, 6, 1, 4, 0, 10, 1, 0, 0, 2, 0, 4, 4, 7, 1, 0, 2, 6, 0, 2, 7, 2, 1, 6, 2, 0, 3, 3, 5, 1, 0, 6, 0, 0, 4, 6, 2, 6, 0, 5, 0, 1, 0, 7, 0, 0, 3, 1, 0, 7, 7, 3, 6, 0, 5, 1, 2, 0, 1, 0, 6, 4, 7, 3, 2, 1, 0, 3, 4, 1, 0, 3, 0, 1, 1, 1, 2, 0, 5, 7, 0, 4, 4, 5, 0, 2, 4, 2, 7, 2, 1, 0, 7, 2, 2, 4, 1, 0, 1, 0, 3, 0, 2, 7, 0, 3, 4, 1, 4, 0, 8, 7, 8, 4, 2, 3, 0, 1, 0, 6, 6, 2, 5, 1, 6, 4, 6, 2, 0, 7, 1, 3, 6, 1, 3, 3, 2, 5, 6, 10, 1, 5, 7, 5, 0, 2, 1, 7, 0, 4, 0, 3, 4, 0, 3, 4, 8, 1, 3, 1, 1, 7, 3, 0, 1, 5, 4, 5, 0, 1, 7, 6, 0, 4, 7, 4, 0, 7, 0, 9, 2, 1, 2, 3, 6, 0, 5, 4, 5, 5, 5, 0, 7, 4, 2, 6, 0, 1, 3, 6, 0, 3, 8, 7, 1, 0, 0, 6, 7, 3, 1, 1, 6, 2, 8, 3, 7, 5, 0, 0, 1]
Średnia: 3.007
Odchylenie standardowe: 2.5735094715193885

Obserwowane częstotliwości: [211 147 145 114 99 87 75 61 37 16 8]
Oczekiwane częstotliwości: [90.90909091 90.90909091 90.90909091 90.90909091 90.90909091 90.90909091
90.90909091 90.90909091 90.90909091 90.90909091 90.90909091]
Wartość Chi-kwadrat: 414.11600000000004
Wartość p (test Chi-kwadrat): 9.299084231183466e-83
Odrzucamy hipotezę o rozkładzie równomiernym.
Podsumowując, wyniki symulacji wskazują na istotne różnice pomiędzy uzyskanymi a teoretycznymi wartościami, co może być użyteczne do analizy i optymalizacji wyników łucznika.