LogoPorównanie metody Eulera i funkcji odeint

Pobierz plik .ipynb

-I- OPIS

Badanie koncentruje się na porównaniu dwóch metod rozwiązywania układów Lotki-Volterry i Lorenza: implementacji metody Eulera oraz wykorzystaniu pakietu scipy.

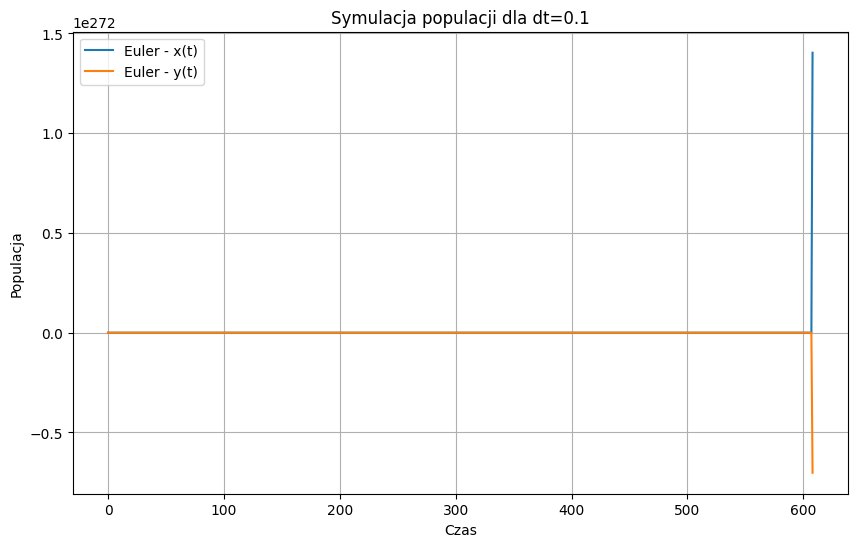
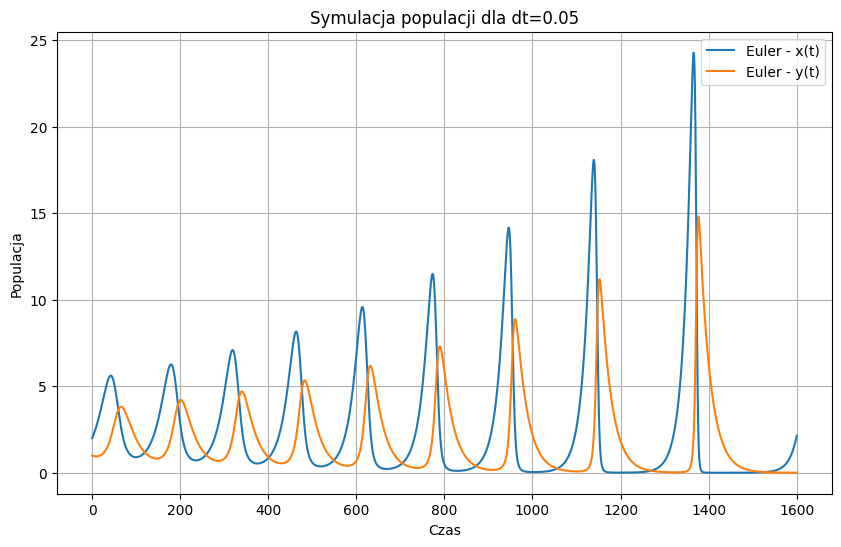
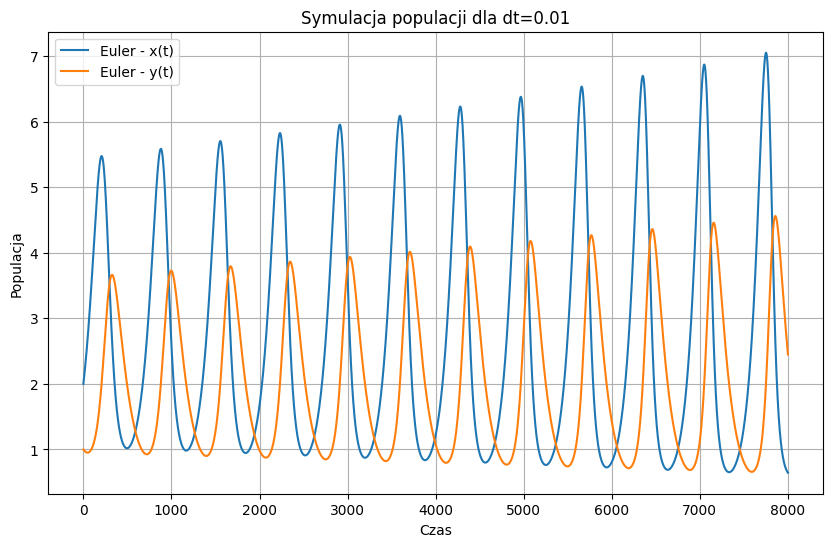
W pierwszej części przeprowadzono symulacje za pomocą metody Eulera. Dokonano porównania wyników dla różnych wartości kroku czasowego (dt). Wyniki zostały przeanalizowane i przedstawione graficznie w celu umożliwienia porównania zachowania układu dla różnych wartości dt.

W kolejnej części raportu wykorzystano inną metodę, korzystając z funkcji odeint z pakietu scipy.integrate. Dodatkowo, dla każdej wartości kroku czasowego użytej w metodzie Eulera, obliczono średni błąd aproksymacji względem wartości referencyjnych uzyskanych za pomocą metody odeint.

Ostateczne wnioski z niniejszego sprawozdania pozwolą na ocenę skuteczności obu metod symulacji oraz ich odporność na dobór kroku czasowego, co jest istotnym czynnikiem wpływającym na dokładność wyników.

-II- Modele

1) Uklad Lotki-Volterry (Równania Dynamiki Populacji)

\[ \begin{cases} \frac{dx}{dt} &= (a - by) \\ \frac{dy}{dt} &= (cx - d)y \end{cases} \]
Równanie dla ofiar (x):

$$ {\frac{dx}{dt} = ax - bxy} $$

Równanie dla drapieżników (y):

$$ {\frac{dy}{dt} = (cx - d)y} $$

System Lorenza (Równania Dynamiki Populacji)

\[ \begin{cases} \frac{dx}{dt} &= \sigma(y - x) \\ \frac{dy}{dt} &= x(\rho - z) - y \\ \frac{dz}{dt} &= xy - \beta z \end{cases} \]
Gdzie:

Symulacja układu Lotki-Volterry w Python (metoda Eulera)

import numpy as np
import matplotlib.pyplot as plt

def euler_method(a, b, c, d, x0, y0, dt, steps):
    x_values = [x0]
    y_values = [y0]
    for _ in range(steps):
        dx_dt = a * x_values[-1] - b * x_values[-1] * y_values[-1]
        dy_dt = c * x_values[-1] * y_values[-1] - d * y_values[-1]
        x_new = x_values[-1] + dx_dt * dt
        y_new = y_values[-1] + dy_dt * dt
        x_values.append(x_new)
        y_values.append(y_new)
    return x_values, y_values

# Funkcja obliczająca średni błąd aproksymacji
def calculate_average_error(true_values, approx_values):
    errors = np.abs(true_values - approx_values)
    return np.mean(errors)

# Parametry
a = 1.2
b = 0.6
c = 0.3
d = 0.8

# Populacje początkowe
x0 = 2
y0 = 1

# Lista różnych wartości kroku dt
dt_values = [0.1, 0.05, 0.01]

# Wyniki metody Eulera dla różnych wartości kroku dt
for dt in dt_values:
    steps = int(80 / dt)
    x_values, y_values = euler_method(a, b, c, d, x0, y0, dt, steps)
    
    plt.figure(figsize=(10, 6))
    plt.plot(x_values, label='Euler - x(t)')
    plt.plot(y_values, label='Euler - y(t)')
    plt.title(f'Symulacja populacji dla dt={dt}')
    plt.xlabel('Czas')
    plt.ylabel('Populacja')
    plt.legend()
    plt.grid(True)
    plt.show()

Porównanie wyników m. Eulera i odeint układu Lotki-Volterry 

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

def euler_method(a, b, c, d, x0, y0, dt, steps):
    x_values = [x0]
    y_values = [y0]
    for _ in range(steps):
        dx_dt = a * x_values[-1] - b * x_values[-1] * y_values[-1]
        dy_dt = c * x_values[-1] * y_values[-1] - d * y_values[-1]
        x_new = x_values[-1] + dx_dt * dt
        y_new = y_values[-1] + dy_dt * dt
        x_values.append(x_new)
        y_values.append(y_new)
    return x_values, y_values

# Funkcja obliczająca średni błąd aproksymacji
def calculate_average_error(true_values, approx_values):
    errors = np.abs(true_values - approx_values)
    return np.mean(errors)

# Parametry
a = 1.2
b = 0.6
c = 0.3
d = 0.8

# Początkowe populacje
x0 = 2
y0 = 1

# Lista różnych wartości kroków dt
dt_values = [0.05, 0.01, 0.001]

# Wyniki metody Eulera dla różnych wartości kroku  dt
for dt in dt_values:
    steps = int(80 / dt)
    x_values_euler, y_values_euler = euler_method(a, b, c, d, x0, y0, dt, steps)
    
    # Rozwiązanie z pomocą odeint
    def model(z, t):
        x, y = z
        dx_dt = a * x - b * x * y
        dy_dt = c * x * y - d * y
        return [dx_dt, dy_dt]
    
    t = np.linspace(0, 80, steps + 1)
    z0 = [x0, y0]
    z_odeint = odeint(model, z0, t)
    x_values_odeint = z_odeint[:, 0]
    y_values_odeint = z_odeint[:, 1]
    
    plt.figure(figsize=(10, 6))
    plt.plot(x_values_euler, label='Euler - x(t)')
    plt.plot(y_values_euler, label='Euler - y(t)')
    plt.plot(x_values_odeint, label='odeint - x(t)', linestyle='--')
    plt.plot(y_values_odeint, label='odeint - y(t)', linestyle='--')
    plt.title(f'Population simulation for dt={dt}')
    plt.xlabel('Time')
    plt.ylabel('Population')
    plt.legend()
    plt.grid(True)
    plt.show()

    error_x = calculate_average_error(x_values_odeint, x_values_euler)
    error_y = calculate_average_error(y_values_odeint, y_values_euler)
    print(f"dt={dt}, Average Error for x(t): {error_x}, Average Error for y(t): {error_y}")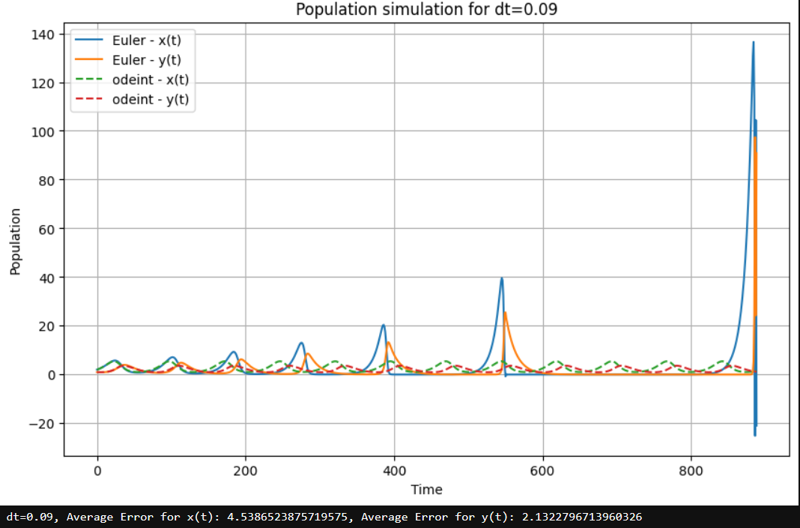

dt=0.09, Average error for x(t): 4.5386523875719575, Average error for y(t): 2.1322796713960326
    

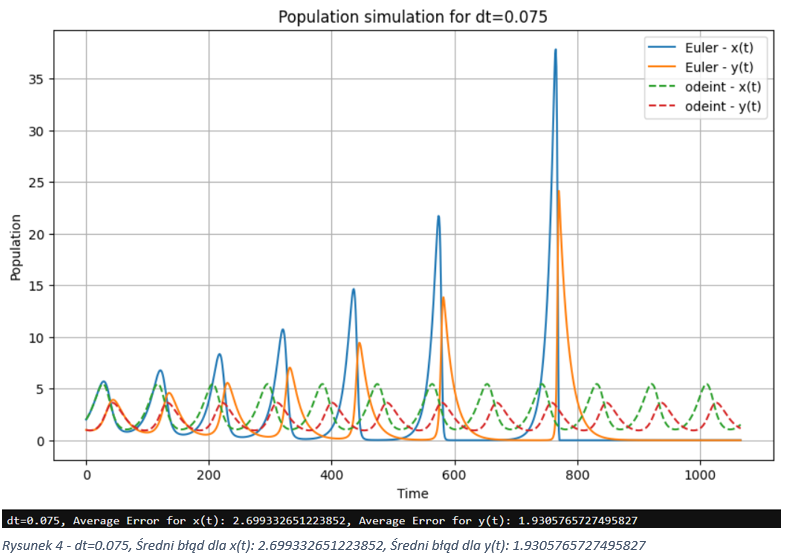
dt=0.075, Average error for x(t): 2.699332651223852, Average error for y(t): 1.9305765727495827
    

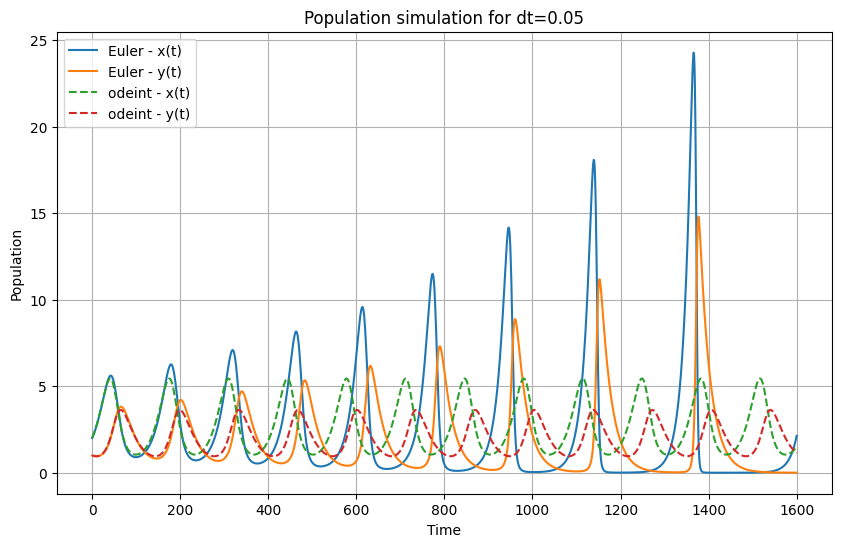
dt=0.05, Average Error for x(t): 2.4437596140948665, Average Error for y(t): 1.583412638014361


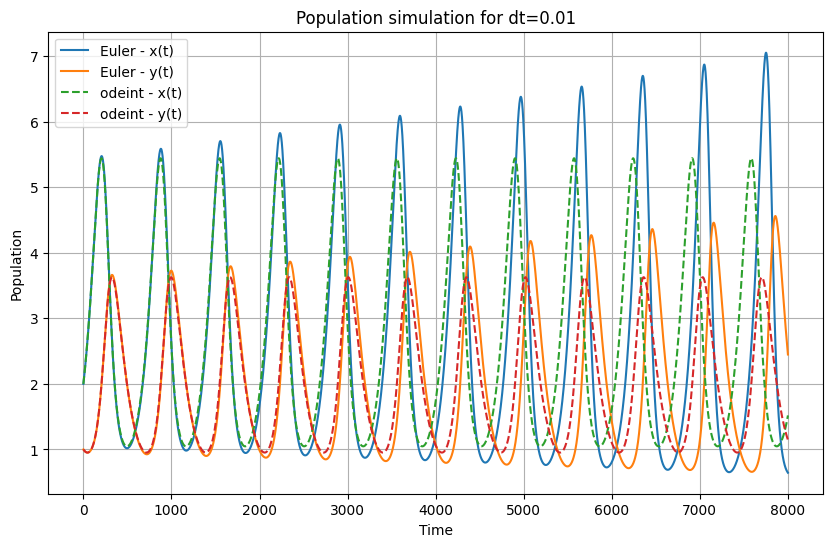
dt=0.01, Average Error for x(t): 0.8149373464424021, Average Error for y(t): 0.5055264320468017


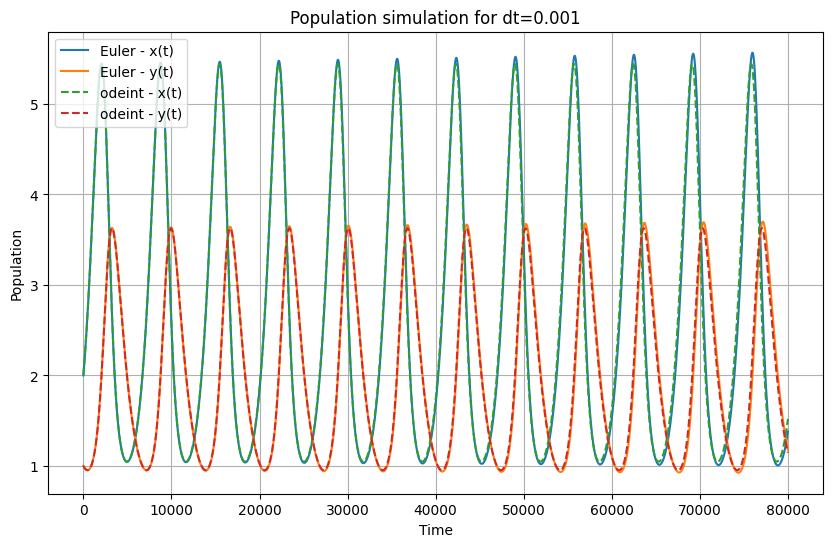
dt=0.001, Average Error for x(t): 0.06583244461491997, Average Error for y(t): 0.04060824939869479

Tabela wyników aproksymacji

dt Średni błąd dla x(t) Średni błąd dla y(t) Średnia (x(t), y(t))
0.09 4.5386523875719575 2.1322796713960326 3.335466029484995
0.075 2.699332651223852 1.9305765727495827 2.3149546119867175
0.05 2.4437596140948665 1.583412638014361 2.013586126054614
0.01 0.8149373464424021 0.5055264320468017 0.6602318892446019
0.001 0.06583244461491997 0.04060824939869479 0.05322034700680738

Porównanie wyników m. Eulera i odeint systemu Lorenza 

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

def euler_method(sigma, rho, beta, x0, y0, z0, dt, steps):
    x_values = [x0]
    y_values = [y0]
    z_values = [z0]
    for _ in range(steps):
        dx_dt = sigma * (y_values[-1] - x_values[-1])
        dy_dt = x_values[-1] * (rho - z_values[-1]) - y_values[-1]
        dz_dt = x_values[-1] * y_values[-1] - beta * z_values[-1]
        x_new = x_values[-1] + dx_dt * dt
        y_new = y_values[-1] + dy_dt * dt
        z_new = z_values[-1] + dz_dt * dt
        x_values.append(x_new)
        y_values.append(y_new)
        z_values.append(z_new)
    return x_values, y_values, z_values

# Funkcja obliczająca średni błąd aproksymacji
def calculate_average_error(true_values, approx_values):
    errors = np.abs(true_values - approx_values)
    return np.mean(errors)

# Parametry modelu Lorenza
sigma = 10
rho = 28
beta = 8/3

# Początkowe warunki
x0 = 0
y0 = 1
z0 = 1.05

# Lista różnych wartości kroku czasowego dt
dt_values = [ 0.04, 0.02, 0.01, 0.001]

# Wyniki dla metody Eulera dla różnych wartości dt
for dt in dt_values:
    steps = int(80 / dt)
    x_values_euler, y_values_euler, z_values_euler = euler_method(sigma, rho, beta, x0, y0, z0, dt, steps)
    
    # Rozwiązanie za pomocą odeint
    def model(state, t):
        x, y, z = state
        dx_dt = sigma * (y - x)
        dy_dt = x * (rho - z) - y
        dz_dt = x * y - beta * z
        return [dx_dt, dy_dt, dz_dt]
    
    t = np.linspace(0, 80, steps + 1)
    state0 = [x0, y0, z0]
    state_odeint = odeint(model, state0, t)
    x_values_odeint = state_odeint[:, 0]
    y_values_odeint = state_odeint[:, 1]
    z_values_odeint = state_odeint[:, 2]
    
    fig = plt.figure(figsize=(16, 5))

    # Wykres y(x)
    plt.subplot(1, 3, 1)
    plt.plot(x_values_euler, y_values_euler, label='Euler', color='blue')
    plt.plot(x_values_odeint, y_values_odeint, label='odeint', color='red', linestyle='--')
    plt.title(f'y(x) - Simulation, dt={dt}')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.legend()
    plt.grid(True)

    # Wykres z(x)
    plt.subplot(1, 3, 2)
    plt.plot(x_values_euler, z_values_euler, label='Euler', color='blue')
    plt.plot(x_values_odeint, z_values_odeint, label='odeint', color='red', linestyle='--')
    plt.title(f'z(x) - Simulation, dt={dt}')
    plt.xlabel('X')
    plt.ylabel('Z')
    plt.legend()
    plt.grid(True)

    # Wykres z(y)
    plt.subplot(1, 3, 3)
    plt.plot(y_values_euler, z_values_euler, label='Euler', color='blue')
    plt.plot(y_values_odeint, z_values_odeint, label='odeint', color='red', linestyle='--')
    plt.title(f'z(y) - Simulation, dt={dt}')
    plt.xlabel('Y')
    plt.ylabel('Z')
    plt.legend()
    plt.grid(True)
    
    plt.tight_layout()
    plt.show()

    fig = plt.figure(figsize=(12, 8))
    ax = fig.add_subplot(111, projection='3d')
    ax.plot(x_values_euler, y_values_euler, z_values_euler, label='Euler', color='blue')
    ax.plot(x_values_odeint, y_values_odeint, z_values_odeint, label='odeint', color='red', linestyle='--')
    ax.set_title(f'Simulation for dt={dt}')
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.legend()
    plt.show()

    error_x = calculate_average_error(x_values_odeint, x_values_euler)
    error_y = calculate_average_error(y_values_odeint, y_values_euler)
    error_z = calculate_average_error(z_values_odeint, z_values_euler)
    print(f"dt={dt}, Average Error for X: {error_x}, Average Error for Y: {error_y}, Average Error for Z: {error_z}")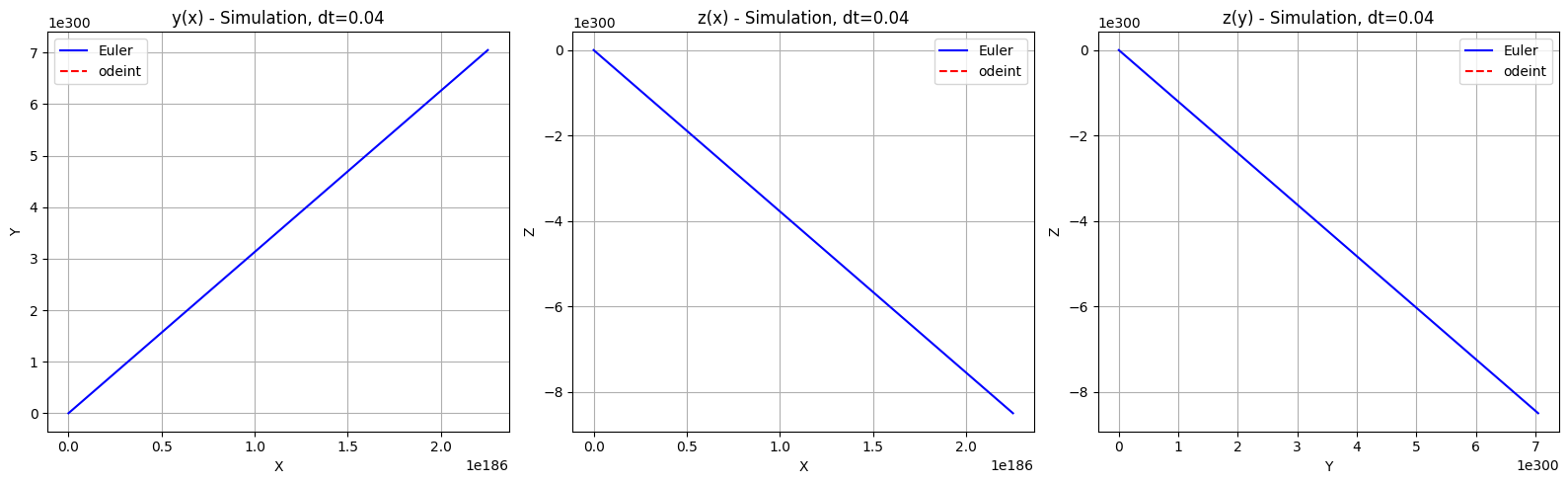

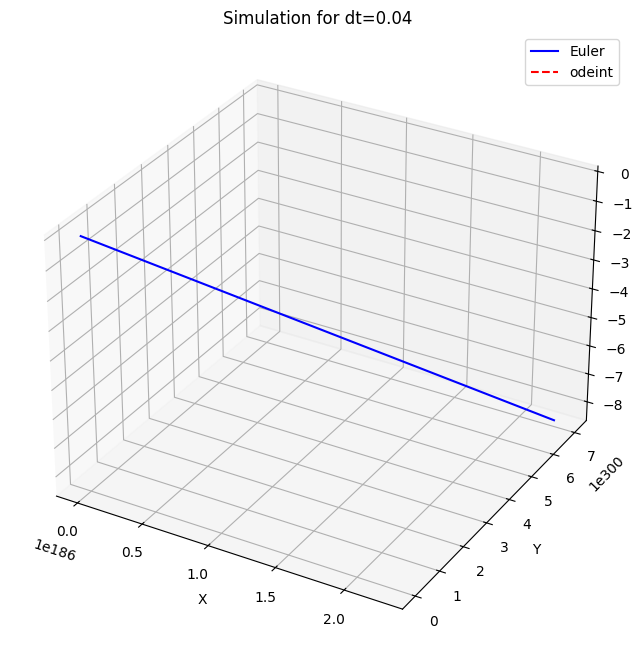
dt=0.04, Average Error for X: nan, Average Error for Y: nan, Average Error for Z: nan


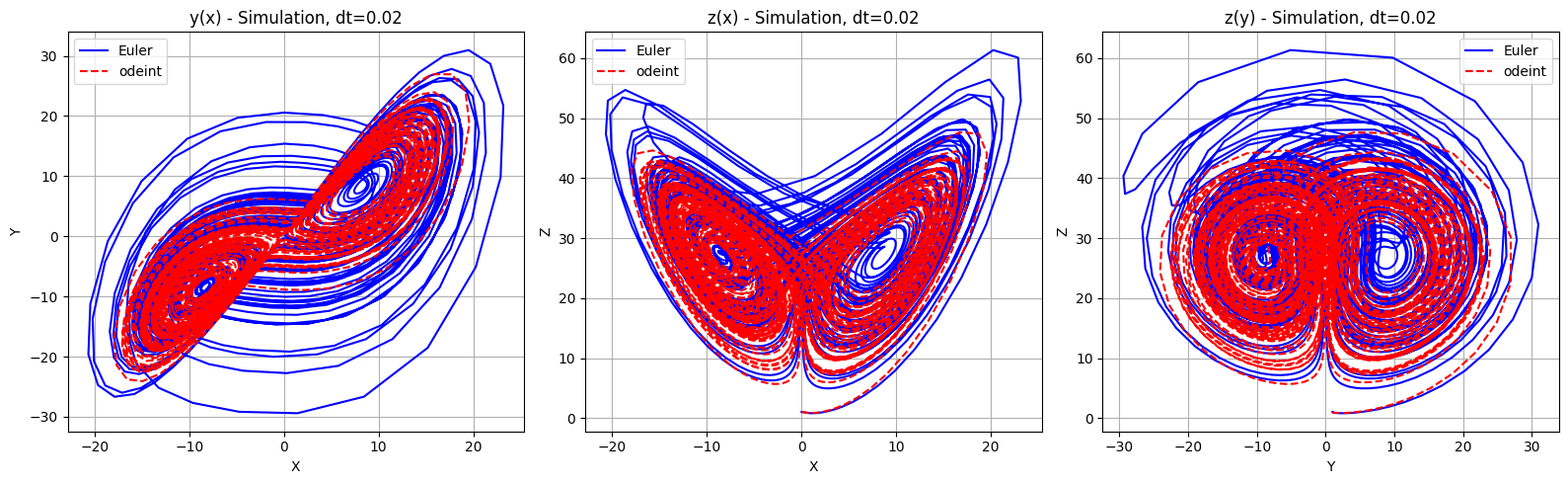
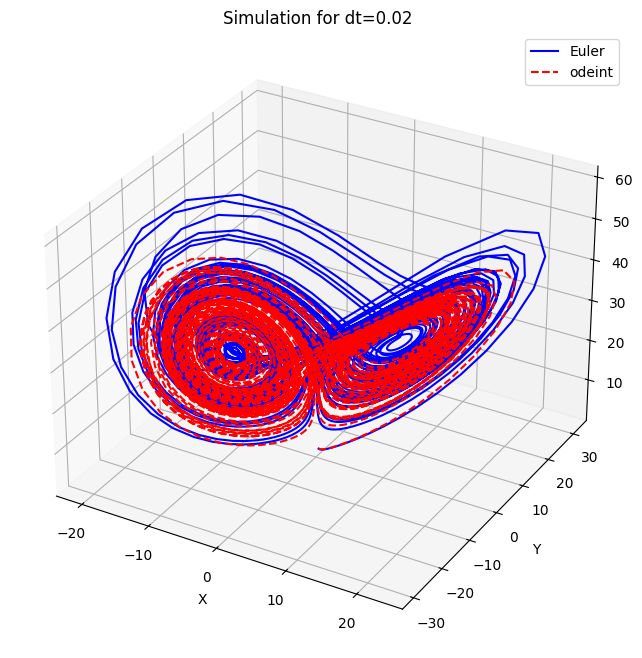
dt=0.02, Average Error for X: 9.160473319570897, Average Error for Y: 10.394051377529555, Average Error for Z: 9.452990585686898


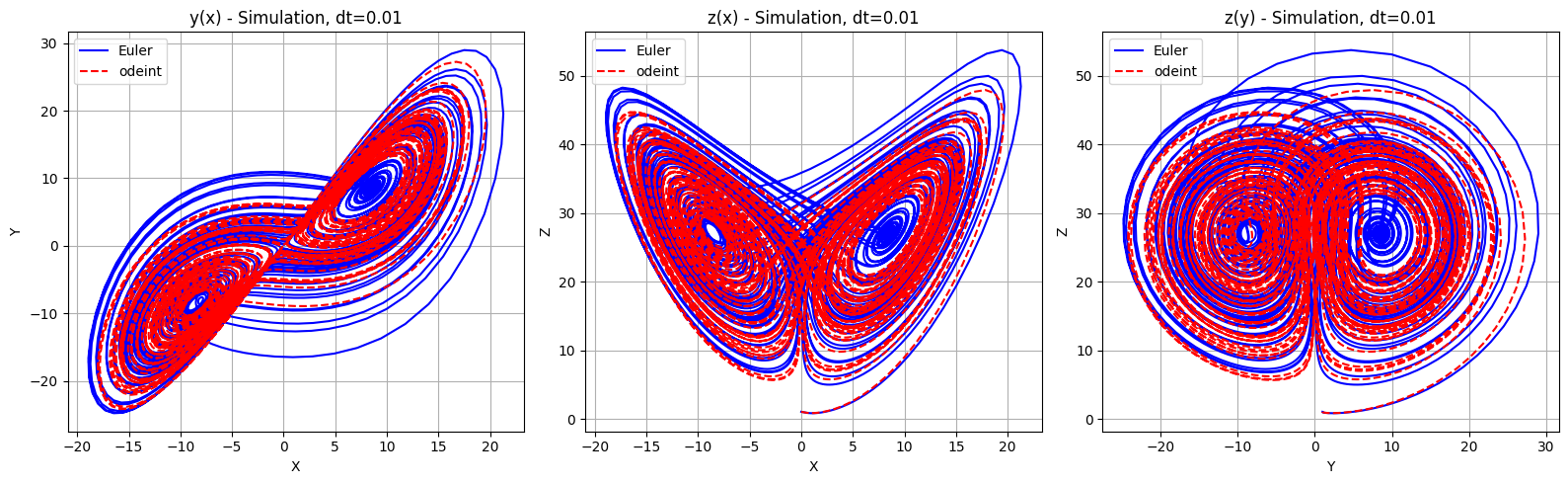
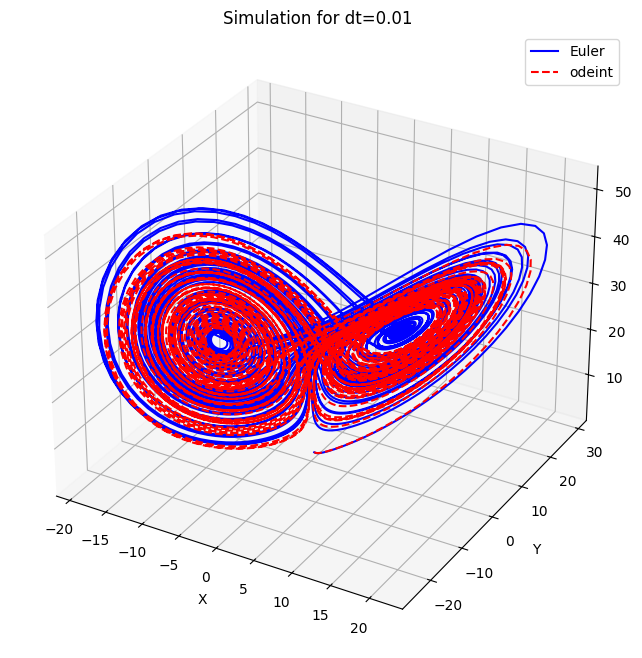
dt=0.01, Average Error for X: 8.581482374633888, Average Error for Y: 9.601881745806123, Average Error for Z: 9.22120213881979


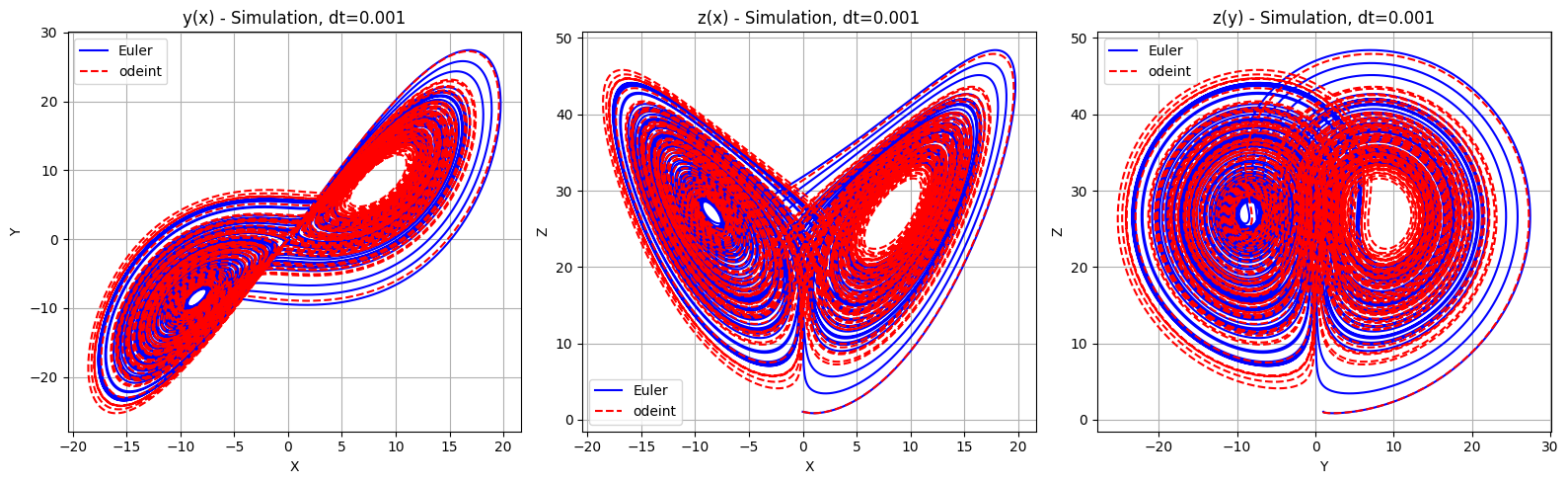
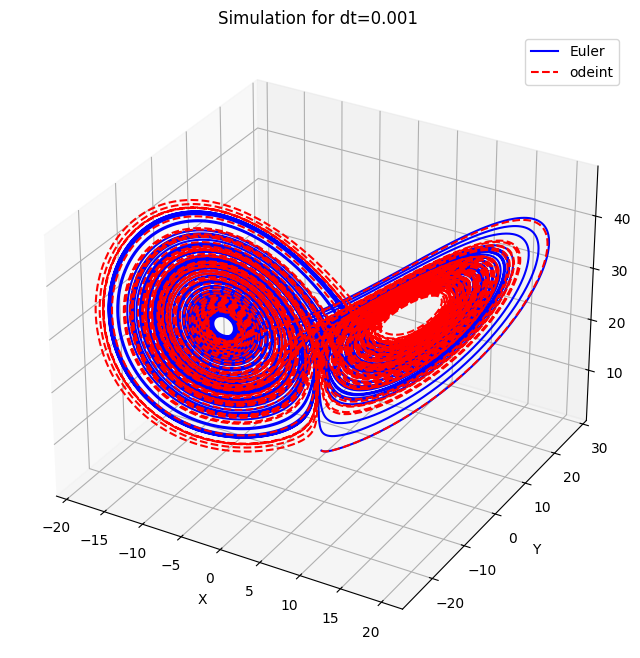
dt=0.001, Average Error for X: 6.946460771812238, Average Error for Y: 7.857654961620313, Average Error for Z: 7.920956509955428

Tabela wyników aproksymacji

dt Średni błąd dla X Średni błąd dla Y Średni błąd dla Z Średnia (x, y, z)
0.02 9.160473319570897 10.394051377529555 9.452990585686898 9.33583876059685
0.01 8.581482374633888 9.601881745806123 9.22120213881979 9.134522419753267
0.001 6.946460771812238 7.857654961620313 7.920956509955428 7.575357414462326

-III- Wnioski z analizy symulacji numerycznych

Model Lotki-Volterru

Analizując dane dotyczące średnich błędów dla różnych wartości kroku czasowego dt dla metod symulacji przy użyciu metody Eulera i odeint, można wyciągnąć następujące wnioski:

System Lorenza

Na podstawie danych dotyczących średnich błędów dla różnych wartości kroku czasowego dt w symulacji systemu Lorenza, można wyciągnąć następujące wnioski:

-IV- Wniosek ogólny:

Metoda odeint jest bardziej dokładną metodą numeryczną niż metoda Eulera w przypadku symulacji dynamiki układów fizycznych, szczególnie dla większych wartości kroku czasowego. Dla małych wartości dt, różnice pomiędzy obiema metodami są mniejsze, ale nadal metoda odeint może zapewniać lepszą dokładność i stabilność.

Dmytro Zavhorodnii ©