Wprowadzenie do trygonometrii sferycznej.

§ 1.1 Kąty i kręgi na kuli.

Kula to ciało utworzone przez obrót półkola wokół swojej średnicy. Geometria sferyczna to dziedzina matematyki zajmująca się badaniem figur geometrycznych leżących na powierzchni kuli. Powstała powierzchnia nazywana jest powierzchnią sferyczną. Często taka powierzchnia nazywana jest po prostu kulą. Zatem kula jest zbiorem punktów w przestrzeni równoodległych od jednego punktu, zwanego środkiem kuli.

Każda płaszczyzna K, przecinająca się z kulą, zakreśli na kuli określony okrąg

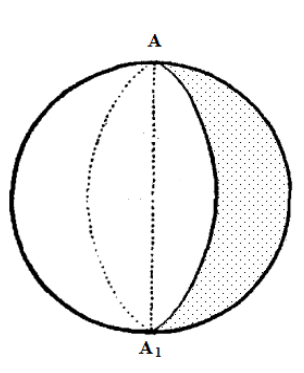
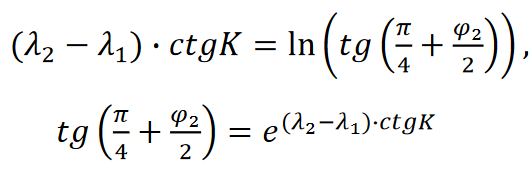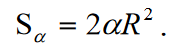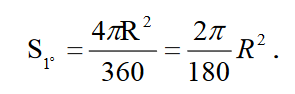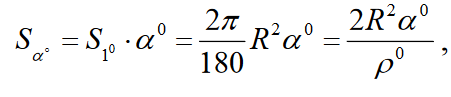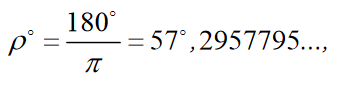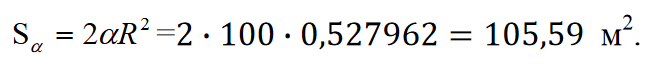Prostopadła do płaszczyzny K średnica kuli przechodząca przez jej środek O przecina kulę w dwóch punktach M i M1, zwanych sferycznymi środkami okręgu. Okręgi, których płaszczyzny przechodzą przez środek kuli O, nazywane są kołami wielkimi ; pozostałe okręgi na kuli nazywane są mniejszymi okręgami. Sferyczne środki M i M1 wielkiego koła nazywane są jego biegunami. Bieguny są oddalone o 90° od odpowiednich kół wielkich lub ćwiartki koła. Rzeczywiście, punkty A i B wielkiego koła leżą na łukach AM i VM1, które są równe 90° .

Przez dwa punkty na kuli, które nie leżą na końcach tej samej średnicy, można narysować łuk koła wielkiego i to w dodatku tylko jednego. Łuk - koło wielkie - to najkrótsza odległość między punktami na kuli. Należy zauważyć, że dwa punkty dzielą okrąg na dwie nierówne części. Mniejszy łuk AB wielkiego koła wyznacza sferyczną (najkrótszą) odległość między punktami A i B na powierzchni kuli. Łuk ten nazywany jest linią geodezyjną. Linie geodezyjne odgrywają na kuli taką samą rolę jak linie proste w planimetrii.

Tabela zawiera szereg analogii między pojęciami związanymi z płaszczyzną i sferą, przydatnych do dalszej nauki.

W trygonometrii sferycznej brane są pod uwagę tylko takie figury, które są utworzone przez łuki wielkich kół, dlatego w dalszej części tekstu słowo „łuk” oznacza odcinek łuku wielkiego koła. W tych przypadkach, jeśli chodzi o łuk małego koła, zostanie to specjalnie określone. Długość łuku jest proporcjonalna do wartości kąta środkowego , czyli kąta opisanego końcem promienia przy przejściu od jednego końca łuku do drugiego, więc łuk na kuli mierzy się kąt między promieniami opartymi na końcach tego łuku.

Z reguły w trygonometrii sferycznej, zgodnie z sugestią Leonharda Eulera, brane są pod uwagę tylko te łuki, których długość jest równa lub mniejsza niż połowa długości koła, to znaczy 180°. Ta reguła nazywa się ograniczeniem Eulera.

Dwa łuki, BB1 i CC1, przecinające się w jednym punkcie A na kuli tworzą kąt sferyczny CAB, który będziemy oznaczać ∠ CAB. gdzie A jest jego wierzchołkiem, a łuki AB i AC są bokami kąta sferycznego. Wartość kąta sferycznego mierzy się jako kąt między stycznymi MA i NA do boków kąta sferycznego CAB w wierzchołku kąta sferycznego.

Dowód:

Ponieważ łuki ABA1 i ACA1 są łukami wielkich okręgów, punkty A i A1 leżą na tej samej średnicy AOA1, reprezentującej linię przecięcia płaszczyzn ABA1 i ACA1. Płaszczyzny te tworzą kąt dwuścienny, który będziemy nazywać odpowiadającym kątowi sferycznemu BAC.

Narysujmy styczne MA i NA do boków kąta sferycznego ABC w jego wierzchołku A. Dzięki własności stycznych leżą one w płaszczyznach kół wielkich ABA1 i ACA1 oraz AM⊥AA1, AN⊥AA1. Narysujmy płaszczyznę przekroju OCBD, prostopadłą do średnicy AA1 i przechodzącą przez środek kuli O. Przecięcie tej płaszczyzny z kulą da koło wielkie BCD, dla którego punkty A i A1 są biegunami. Okrąg ten przecina się z łukami ABA1 i ACA1 w punktach B i C. Zgodnie z konstrukcją OB⊥AA1 i OC⊥AA1 . Zatem kąt BOC będzie również kątem płaskim kąta dwuściennego MAA1N, a ponieważ wszystkie kąty płaskie kąta dwuściennego są równe, ∠ BOC = ∠ MAN = ∠ BAC

Ponieważ kąt BOC jest środkowym kątem łuku ∠ BOC = ∪ BC ==> ∠ BAC = ∪ BC, cnd.

Wniosek 1. Kąt sferyczny i odpowiadający mu kąt dwuścienny mają tę samą miarę

Wniosek 2. Łuk koła wielkiego przechodzący przez biegun innego koła wielkiego jest prostopadły do ​​tego koła wielkiego. ∪ AB = ∪ BC ( rys. )

Łuk ∪AB nazywamy sferyczną prostopadłą do łuku ∪BC, ponieważ kąt między łukami wynosi 90°

Wniosek 3. Sferyczna prostopadła do danego łuku wielkiego koła przechodzi przez biegun tego wielkiego koła

Dowód:

Prosta OB leży w płaszczyźnie CODB, która jest prostopadła do prostej AA1. Przez dwie proste AO i OB, przecinające się w punkcie O, rysujemy płaszczyznę AOA1B. Ta płaszczyzna jest prostopadła do płaszczyzny CODB. Na przecięciu z kulą płaszczyzna tworzy łuk koła wielkiego ABA1. Zgodnie z Wnioskiem 2 łuk przechodzący przez biegun jakiegoś innego koła wielkiego jest prostopadły do ​​tego koła wielkiego, co dowodzi Wniosku 3.

Wniosek 4. Pionowe kąty sferyczne są sobie równe

Wniosek 5. Suma sąsiednich kątów sferycznych wynosi 180°.

§ 1.2 Pomiar łuków i kątów środkowych

Następujące jednostki są używane do pomiaru długości łuków i odpowiadających im kątów środkowych:

Zależność miary kątowej (stopień), radianowej i liniowej łuku wielkiego koła określa wzór:

L, α, α° - liniowa, radianowa i kątowa miara łuku koła wielkiego; R - jest promieniem kuli; ρ° - liczba jednostek kąta w radianie ρ° = 180°/π = 57,2957795°.

Zależność miary radianowej od liniowej miary łuku małego koła przechodzącego przez punkt D leżący na łuku BD o kącie środkowym φ od ΔODO1 określa wzór:

§ 1.3. Układ współrzędnych geograficznych sferycznych

Położenie punktu na powierzchni kuli (na przykład kuli ziemskiej) określa się za pomocą współrzędnych geograficznych: szerokości i długości geograficznej. Równoleżniki i południki tworzą układ współrzędnych siatki na powierzchni Ziemi, za pomocą którego można precyzyjnie określić dowolny punkt na Ziemi. Szerokość i długość geograficzna to odpowiednio współrzędne równoleżników i południków, które są mierzone w stopniach i reprezentują odległości kątowe obliczone od środka Ziemi do jej powierzchni względem równika w pionie (na szerokości geograficznej - φ) i względem zera południk poziomo (na długości geograficznej - λ).

Szerokość geograficzna φ jest mierzona odległością sferyczną wzdłuż południka od równika do odpowiedniego równoleżnika φ=NM (północ lub południe od 0° do 90°). Długość geograficzną mierzy się pod kątem λ od głównego południka do odpowiedniego południka (wschód lub zachód od 0° do 180°).

Zatem punkt M na kuli ziemskiej jest określony przez współrzędne:

Współrzędne punktu są zwykle zapisywane w stopniach, minutach i sekundach. Do kolejnych obliczeń zaleca się przepisanie współrzędnych punktu w stopniach jako ułamek dziesiętny oraz w radianach. Jest to wygodny zapis przy stosowaniu wzorów trygonometrycznych.

Rozważmy dwa dowolne punkty M1 i M2 na powierzchni kuli. Azymut punktu M2 względem punktu M1 to kąt sferyczny μ21, który tworzy ortodrom M1M2 oraz mniejszy łuk południka PM1P1, przechodzący przez punkt M1 ( rys ).

Rozwiązanie.

Aby przeliczyć współrzędne ułamka dziesiętnego, używamy wzoru ( 1.Stopień ):

Szerokość: 49°58′50” =49 + (58/60 + 50/3600)= 49,98056°;

Długość: 36°15′9” =36 + (15/60 + 9/3600)= 36,2525°;

Aby obliczyć współrzędne w radianach, używamy wzoru ( 2. Radian ):

Szerokość: 49,98056° * (π/180°) = 0,872325;

Długość: 36,2525° * (π/180°) = 0,632725;

Dzięki Internetowi problem ten można łatwo rozwiązać za pomocą kalkulatora online.

§ 1.4. Loxodroma

Loxodroma (lub loxodromia) - krzywa na powierzchni obrotu przecinająca wszystkie południki pod stałym kątem K, który nazywa się kątem toru loksodromu. Pojęcie to zostało wprowadzone przez portugalskiego matematyka Noniusza w 1529 roku.

Na powierzchni Ziemi loxodromy to wszystkie równoleżniki (K=±90°) i wszystkie południki (K=0° i K=180°). Pozostałe loxodromy to spirale, wykonujące nieograniczoną liczbę obrotów, zbliżające się do biegunów. Jeśli podróżnik porusza się wzdłuż dowolnego loxodromu (z wyjątkiem równoleżników) ze stałą prędkością bez zatrzymywania się, to na pewno dotrze do jednego z biegunów w skończonym czasie.

Loxodrome jest szeroko stosowany w nawigacji morskiej i lotniczej, gdzie kąt K jest interpretowany jako rzeczywisty kurs statku lub samolotu. Zastosowanie loxodromu zamiast ortodromu (reprezentującego najkrótszą odległość między dwoma punktami na kuli) wynika z praktycznej wygody sterowania statkiem lub samolotem, chociaż w tym przypadku droga jest dłuższa. Loxodrome jest czasami używany w geodezji sferycznej.

Niech promień Ziemi będzie równy R, a promień jakiegoś równoległego AB - r. Następnie wyrażenie r = Rcos(φ). Niech łuk М0С będzie loxodromem z dwoma sąsiednimi dowolnymi punktami M1 (φ1 ,λ1) i М2 (φ2 ,λ2); K - kąt przecięcia loxodromu z południkami ziemi. Długość łuku równoleżnika MM2 i długość łuku południka MM, które są zawarte między tymi dwoma punktami, wyznacza się na podstawie długości promieni i wartości kąta środkowego.

Δλ = λ2 - λ1 Trójkąt M1MM2 ze względu na swoją małość można uznać za płaski, dodatkowo kąt M jest równy 90°, zatem

Przejdźmy od elementarnych małych przyrostów do nieskończenie małych: Δφ = dφ, Δλ = dλ

Wtedy tgK = dλ * cosφ/dφ , stąd dλ = tgK * dφ/cosφ

Rozwiązujemy otrzymane równanie różniczkowe:

Obliczając całki, otrzymujemy

Z trójkąta M1MM2 wynika również, że M2M1 = MM1/cosK, ale skoro MM1 = Rdφ, to długość łuku M2M1 loxodrome oblicza się ze wzoru

Z analizy równań można wyciągnąć następujące wnioski.

1. Gdy К=0° lub К=180° wynika z tego, że tgК= 0. Wtedy Δλ = λ2 - λ1 = 0 ==> λ2 = λ1, to znaczy loxodrom pokrywa się z południkiem .

2. Gdy K = 90° lub K = -90°, wynika z tego, że tgK dąży do nieskończoności; a jest to możliwe, jeśli mianownik ułamka po prawej stronie jest równy zeru, φ2 = φ1 . W takich przypadkach loksodrom pokrywa się z równoleżnikiem

   W szczególnym przypadku, przy φ2 = φ1 = 0°, loksodrom pokrywa się z równikiem.

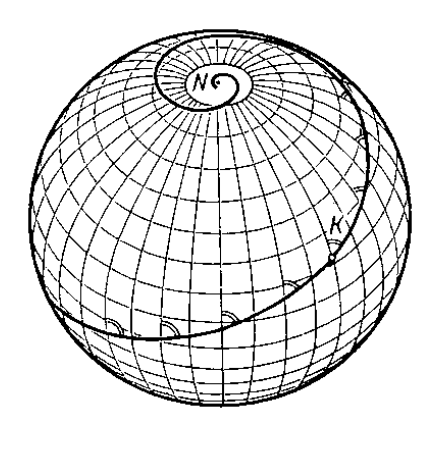
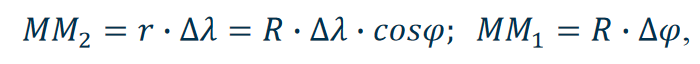
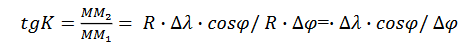
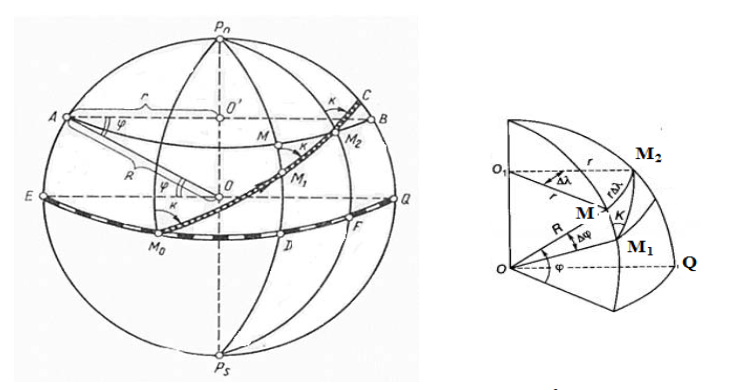
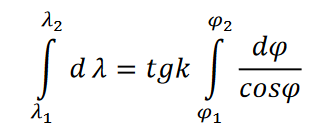
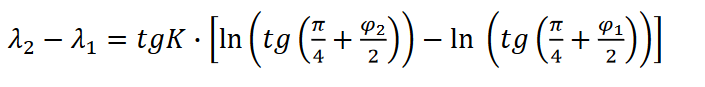
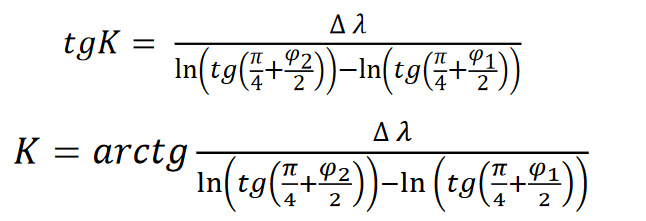
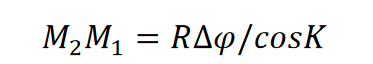
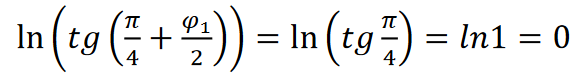3. Niech φ1 = 0°, wtedy a równanie loksodromu przyjmie postać:

Podstawiając wartości λ2 co 360° (okrążając świat wzdłuż loxodromu), widać, że każdej nowej wartości długości geograficznej odpowiada nowa wartość szerokości geograficznej. Innymi słowy, loksodrom przecina każdy południk niezliczoną ilość razy, ale za każdym razem na nowej szerokości geograficznej.

Gdy tangens dąży do nieskończoności: π/4 + φ2/2 = π/2

Zaleca się ustawienie długości geograficznej Hawany jako ujemnej -82°21', ponieważ jej długość mierzona jest na zachód (W).

Przeliczmy na radiany ( kalkulator )

§ 1.5 Sferyczny dwukąt.

Na powierzchni kuli zwykle uważa się figury utworzone przez przecięcie łuków wielkich kół kuli. Najprostszą figurą jest kulisty digon - część powierzchni kuli, która jest ograniczona dwoma dużymi półkolami. Boki kulistej przekątnej, złożonej z półokręgów wielkich kół, są równe 180° każdy. Na przykład na rysnku AA1 będzie kulistym digonem. Ponieważ kąt liniowy kąta dwuściennego między dwiema płaszczyznami jest utworzony przez dwie proste leżące w obu płaszczyznach i prostopadłe do linii ich przecięcia w tym samym punkcie, możemy zdefiniować kąt kulistego wielokąta jako kąt między dwoma styczne do dużych okręgów dwukąta przechodzącego przez jego wierzchołek.

Na podstawie tych definicji łatwo jest udowodnić:

TWIERDZENIE: 1. Pole dwukąta o kącie α leżącym na kuli o promieniu R jest określone wzorem.

Jeśli pole powierzchni kuli podzielimy na 360 równych części, to każda z nich będzie równa polu przekątnej, której wierzchołek ma kąt równy 1°:

Wtedy pole dwukąta o kącie α° równa się:

α° =30°15' = 30,25°, w radianach a = 0,527962

Wtedy pole dwukąta wynosi:

§ 1.6 Pytania i ćwiczenia

1. Co bada geometria sferyczna?
2. Co to jest ortodrom?
3. Co to jest loksodromia?
4. Jaka zależność określa zależność między miarą kątową (stopień, radian) a miarą liniową łuku koła wielkiego?
5. Czym jest „sferyczny środek” i „sferyczny promień” małego koła?
6. Jak określa się położenie punktu w kulistym układzie współrzędnych geograficznych?
7. Jaka jest istota ograniczeń Eulera?
8. Jakich wzorów używa się do obliczenia liniowej długości łuku dużego i małego koła?
9. W jaki sposób powiązane są miary stopni i radianów łuków i kątów?
10. Podaj w radianach (z dokładnością do siódmego miejsca po przecinku) kąt sferyczny mierzony w stopniach: φ1 = 42°54'6", φ2 = 160°9'47" (odp: φ1 = 0,7487753, φ2 = 2,7953727)
11. Podaj w miarę liniową (z dokładnością do km) łuk S koła wielkiego kuli ziemskiej (R = 6370 km), mierzony w stopniach: φ1 = 63°0'42" (Odp: S = 7006km)
12. Co to jest „kąt sferyczny” i jak się go mierzy?
13. Jak obliczyć pole kulistego dwukąta?