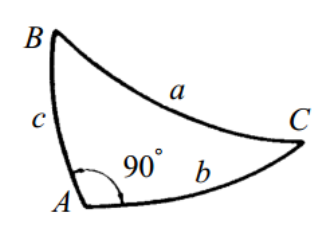
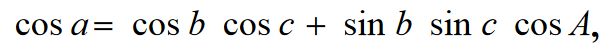§ 4.2 Związek między bokami i kątami.
- Aby połączyć przeciwprostokątną i przyprostokątne, mamy sferyczny wzór Pitagorasa:
- Niech każda z przyprostokątnych będzie mniejsza niż 90°, wtedy cos(b) i cos(c) są dodatnie, ale wtedy cos(a) jest również dodatnie, a zatem a < 90° .
- Jeśli każda z przyprostokątnych jest większa niż 90°, to cos(b) i cos(c) są ujemne, a zatem cos a jest dodatnie, a a < 90°.
- Jeśli jedna z przyprostokątnych jest większa niż 90°, a druga mniejsza niż 90°, to cosinus jednej z przyprostokątnych jest dodatni, a drugiej ujemny. Dlatego cos a będzie ujemne, a a > 90°.
-
Aby połączyć przeciwprostokątną z sąsiednimi kątami, mamy zależność
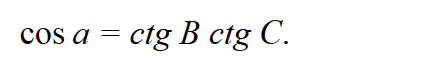Po przeanalizowaniu tego wyrażenia podobnie do analizy wzoru pitagorejskiego ustalamy następujący związek między przeciwprostokątną a sąsiednimi kątami: jeśli kąty przylegające do przeciwprostokątnej są jednorodne, wówczas przeciwprostokątna jest mniejsza niż 90 °; jeśli te kąty są niejednorodne, to przeciwprostokątna jest większa niż 90 ° .
- Aby połączyć jedną z przyprostokątnych i dwa kąty sąsiadujące z przeciwprostokątną, mamy zależność:
Dla wygody umawiamy się, że dwa elementy trójkąta nazywamy jednorodnymi , jeśli oba są większe lub mniejsze niż 90°, a niejednorodnymi , gdy jeden z nich jest większy, a drugi mniejszy niż 90°.
Korzystając z tych pojęć, związek między wartościami przyprostokątnych a przeciwprostokątną można sformułować w następujący sposób: jeśli przyprostokątne są jednorodne, wówczas przeciwprostokątna jest mniejsza niż 90 °; jeśli przyprostokątne są niejednorodne, wówczas przeciwprostokątna jest większa niż 90 ° .
Ponieważ sin(C) jest zawsze dodatni, niezależnie od tego, czy C jest kątem ostrym, czy rozwartym, znaki cos(B) i cos(b) zawsze się pokrywają: dowolna przyprostokątna i jej przeciwny kąt są zawsze jednorodne .
Uzyskane stosunki między wartościami boków i kątów prostokątnego trójkąta sferycznego pomogą, znajdując elementy trójkąta według ich sinusów, wybrać, która z dwóch możliwych wartości elementu jest akceptowalna. Na przykład, jeśli w trójkącie prostokątnym ABC ramię b > 90° i rozwiązując zadanie dla przeciwległego kąta B otrzymamy, że sinB = 0,5, to jego wartość jest równa B = 150°.
§ 4.3 Podstawowe przypadki i instrukcje
Możliwych jest sześć różnych przypadków rozwiązania trójkątów prostokątnych, pod warunkiem, że mamy padane:
- przeciwprostokątna i przyprostokątna;
- dwie przyprostokątnych;
- przeciwprostokątna i kąt do niej przylegający;
- przyprostokątna i kąt do niej przylegający;
- dwa kąta;
- przyprostokątna i jej przeciwny kąt.
Jeśli istnieje rozwiązanie trójkąta, to w pierwszych pięciu przypadkach jest ono unikalne, aw szóstym jest dwuwartościowe. W szóstym przypadku pierwszy z trzech wymaganych elementów jest obliczany przez sinus, który ma wartość dodatnią w pierwszej i drugiej ćwiartce. Dlatego dla pierwszego elementu otrzymujemy dwie wartości, które uzupełniają się aż do 180°. Geometrycznie oznacza to, że mamy dwa sprzężone prostokątne trójkąty sferyczne. Mają dany wspólny bok i przeciwny do niego kąt w wierzchołku przekątnej.
Podczas rozwiązywania należy kontrolować poprawność obliczeń i upewnić się, że wartości elementów spełniają warunki istnienia trójkąta sferycznego.
Instrukcje rozwiązywania prostokątnych trójkątów sferycznych:
Podano przeciwprostokątną a i nogę b. Znajdź nogę c, kąty A i B oraz pole trójkąta.
Spośród dziesięciu formuł wybierzemy następujące
Następnie nieznane elementy są określane za pomocą wzorów
Następnie sprawdźmy poprawność rozwiązania sprawdzając warunki istnienia sferycznego trójkąta prostokątnego.
- 90º < B + C < 270°; −90 < B − C < 90:
- 0< a+b+c < 360°:
- a+b>c, a + c > b, b+c> a, b > c-a, a >b-c, c>b-a:
- Dowolna noga i przeciwległy do niej kąt są zawsze jednorodne.
- Jeśli nogi są jednorodne, przeciwprostokątna musi być mniejsza niż 90º
- Formuła kontrolna musi łączyć znalezione elementy cos(C) = sin(B)cos(c) .
Podano dwie nogi b i c. Znajdź przeciwprostokątną a, kąty B i C.
Spośród dziesięciu formuł wybierzemy następujące
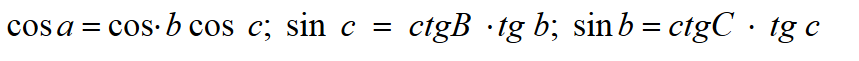
Następnie nieznane elementy są określane za pomocą wzorów:
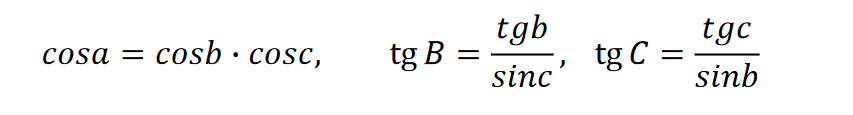
Formuła kontrolna musi łączyć znalezione elementy. Sprawdźmy równość cos(a) = ctg(B)ctg(C)
Podano przeciwprostokątną a i przylegający do niej kąt C. Znajdź nogi i kąt B.
Spośród dziesięciu formuł wybierzemy następujące
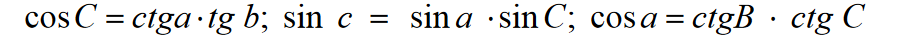
Następnie nieznane elementy są określane za pomocą wzorów:
Formuła kontrolna musi łączyć znalezione elementy. Sprawdźmy równość sin(c) = ctg(B)tg(b)
Dana noga b i przylegający do niej kąt C. Znajdź nogę c, przeciwprostokątna a i kąt B.
Spośród dziesięciu formuł wybierzemy następujące
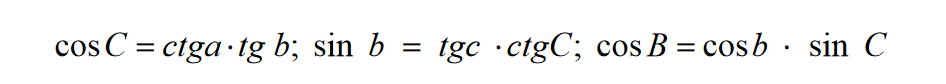
Następnie nieznane elementy są określane za pomocą wzorów:
Formuła kontrolna musi łączyć znalezione elementy. Sprawdźmy równość cos(B) = tg(c)/tg(a)
Dane kąty B i C. Znajdź nogi i przeciwprostokątną.
Spośród dziesięciu formuł wybierzemy następujące
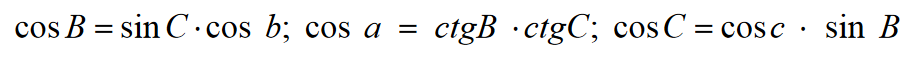
Następnie nieznane elementy są określane za pomocą wzorów:
Formuła kontrolna musi łączyć znalezione elementy. Sprawdźmy równość cos(a) = cos(b)cos(c)
Biorąc pod uwagę nogę b i przeciwległy do niej kąt B. Znajdź nogę c i przeciwprostokątną a, kąt C.
Spośród dziesięciu formuł wybierzemy następujące
Następnie nieznane elementy są określane za pomocą wzorów:
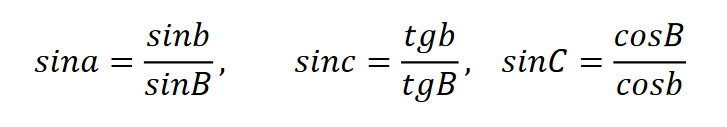
Formuła kontrolna musi łączyć znalezione elementy. Sprawdźmy równość sin(c) = sin(a)sin(C)
Aby trójkąt istniał, sina, sinc i sinC muszą być dodatnie i mniejsze niż jeden. Wymaga to, aby b i B były jednorodne — oba są większe niż 90° lub mniejsze niż 90%. Aby spełnić nierówność sina < 1, konieczne jest, aby sinb było mniejsze niż sinB. Opierając się na fakcie, że b i B muszą znajdować się w tej samej ćwiartce, dla b < 90° b < B < 90° musi być spełniony, a dla b > 90° warunek 90° < b < B.
Jeżeli zadanie jest możliwe, to otrzymujemy dwa rozwiązania, mamy dwa trójkąty sferyczne. Boki a1, c1 i kąt C pierwszego trójkąta będą dopełnieniami odpowiednich boków drugiego trójkąta a2, C2 i kąta C2 aż do 180°. Te trójkąty będą miały wspólną nogę b, a kąty przeciwległe do tej nogi będą równe B.
§ 4.4 Pytania i ćwiczenia
- Co to jest „prostokątny trójkąt sferyczny”? Jakie są jego elementy
- Sformułuj twierdzenie Pitagorasa dla prostokątnych trójkątów sferycznych.
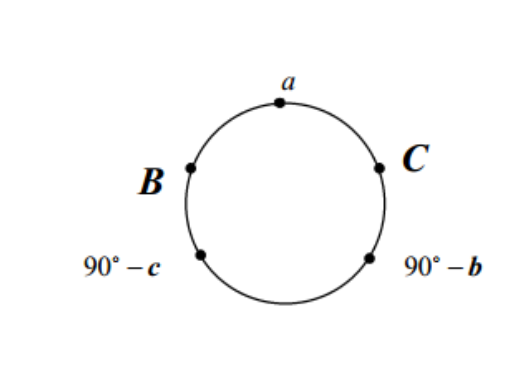
- Sformułuj regułę Napiera.
- Korzystając z reguły Napiera, napisz wzory odnoszące się do następujących elementów trójkąta prostokątnego: a, B, C; a, B, c; ABC; b, b, c; a, c, C; B, c, C.
- Jakie dwa elementy prostokątnego trójkąta sferycznego nazywamy jednorodnymi?
- Jak połączyć przeciwprostokątną z sąsiednimi kątami?
- Jak połączyć nogę z dwoma narożnikami B i C?
- Zapisz warunki istnienia trójkąta sferycznego prostokątnego.
- Ile jest możliwych przypadków rozwiązania trójkąta sferycznego prostokątnego?
- Wykonaj schematy obliczeniowe dla każdego przypadku rozwiązywania prostokątnych trójkątów sferycznych.
- Czy trójkąt sferyczny prostokątny jest możliwy, jeśli jego kąty są równe: B=135° , C=140°?
- Czy trójkąt sferyczny prostokątny jest możliwy, jeśli jego kąty są równe: B=35°, C=48°?
- Jak kontrolować poprawność rozwiązywania zadań wyznaczania nieznanych elementów trójkąta sferycznego prostokątnego?