Temat - III.

Podstawowe wzory na trójkąty sferyczne.

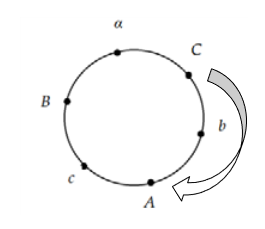
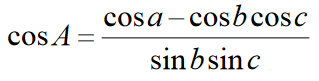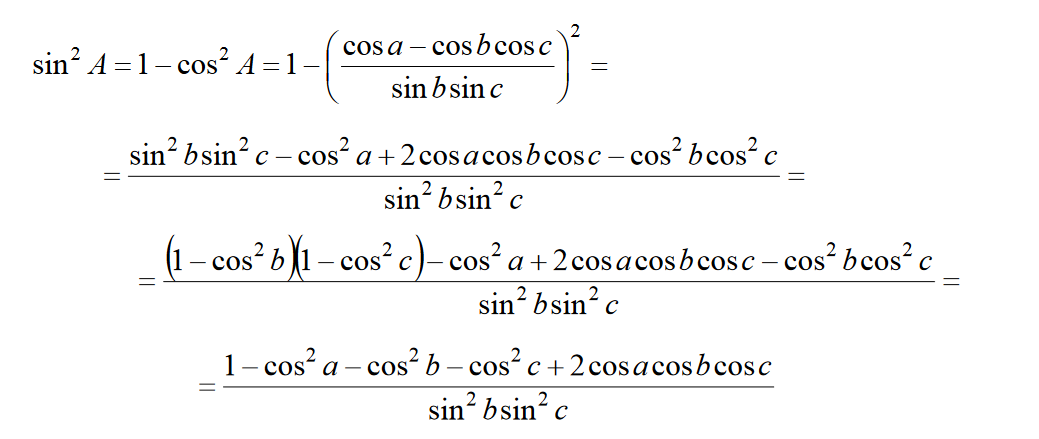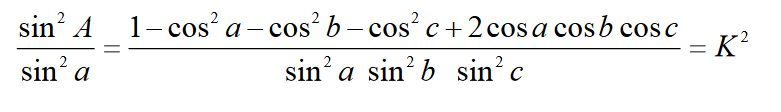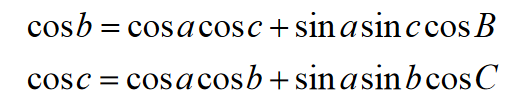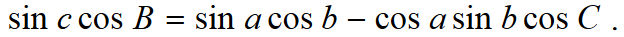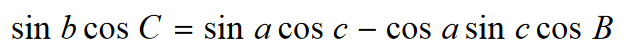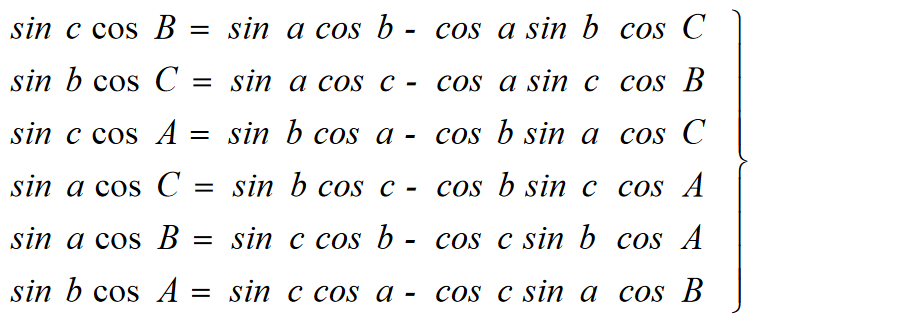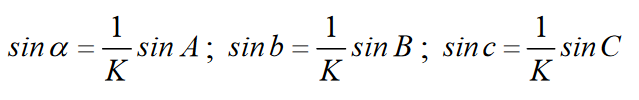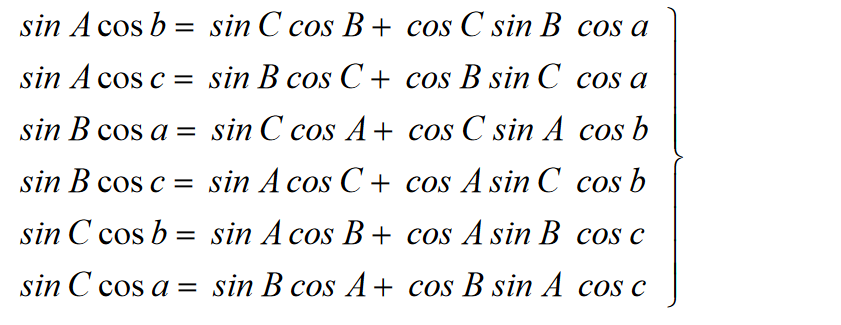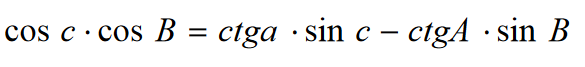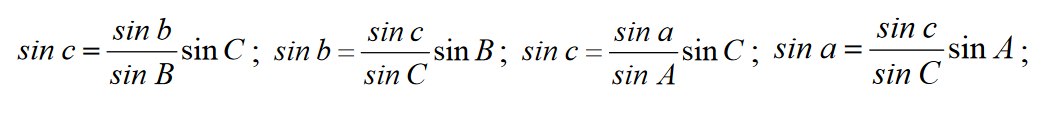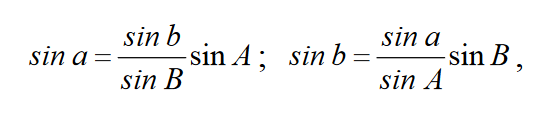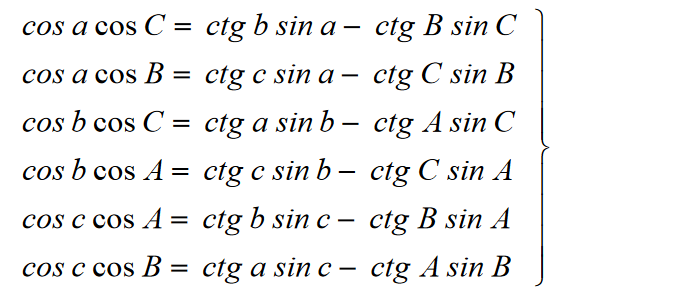§ 3.1 Wzory na cosinusy boków i kątów trójkąta sferycznego

Rozważmy, który przedstawia trójkąt ABC na kuli o promieniu równym jeden i środku w punkcie O. W wierzchołku A poprowadzono styczne AE i AD do boków c i b trójkąta sferycznego. Styczne te przecinają się w punktach E i D z przedłużeniem promieni kuli, które przechodzą przez wierzchołki B i C.

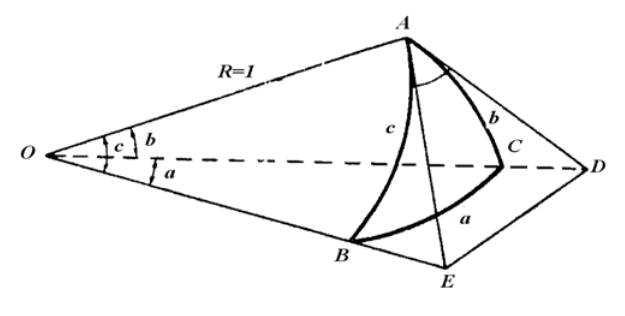Stosujemy twierdzenie cosinusów dla płaskich trójkątów AED i OED:

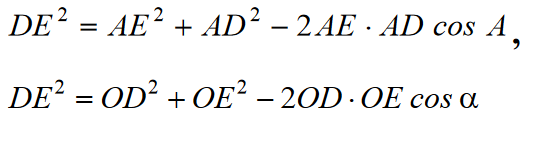
Przyrównując prawe strony równań, otrzymujemy:

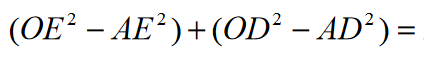
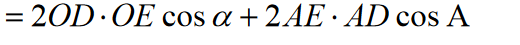
Biorąc pod uwagę, że promień kuli jest równy jeden, z trójkątów prostokątnych OAE OAD otrzymujemy:

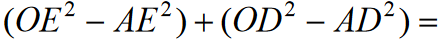
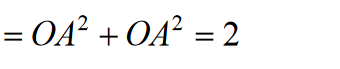
Ponieważ

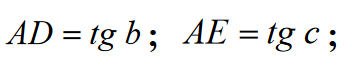
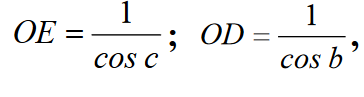
otrzymujemy:

Mnożymy wszystkie warunki ostatniego równania przez cosb * cosc i ostatecznie mamy:

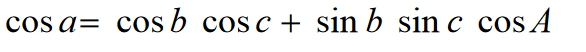
Budowa jest możliwe, jeśli każdy z boków b i c jest mniejszy niż 90°. Dlatego wyrażenie należy uogólnić na przypadek, gdy trójkąt ma boki większe niż 90°.

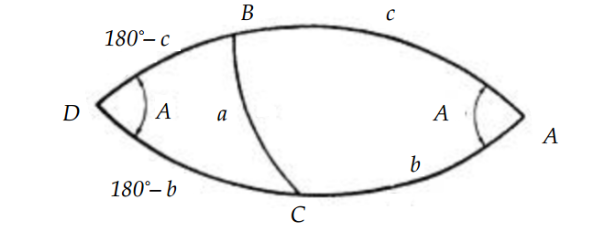
W tym celu rozważ rys . Pokazuje ABC, który ma boki b>90° i c>90°. Jeśli będziemy kontynuować te boki, aż przetną się w punkcie D, to otrzymamy sąsiedni trójkąt DBC, w którym każdy z boków 180° − b i 180° − c jest mniejszy od 90°.

Następnie dla trójkąta DBC formuła przyjmuje postać

cos(a) = cos(180° − b)cos(180° − c)+sin(180° − b)sin(180° − c)*cos A

albo:

cos(a) = cos(b)cos(c)+sin(b)sin(c)*cos A

W końcu dostajemy:

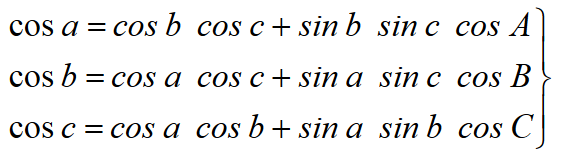
Zatem cosinus boku trójkąta sferycznego jest równy sumie iloczynów cosinusów pozostałych dwóch boków i sinusów tych samych boków, pomnożonej przez cosinus kąta między nimi.

Aby otrzymać wzory na cosinusy kątów trójkąta sferycznego, zapisujemy stosunki boków trójkąta A1B1C1, który jest biegunowy względem trójkąta ABC:

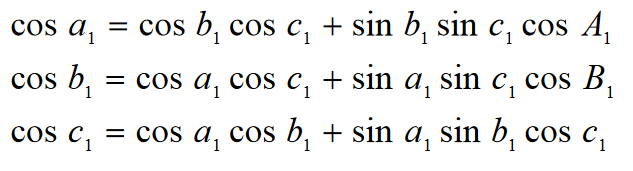
Zgodnie z główną właściwością wzajemnie biegunowych trójkątów ABC i A1B1C1:

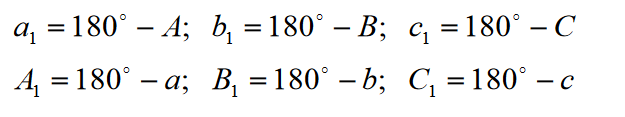
Podstawienie tych równości do poprzedniego wzoru daje

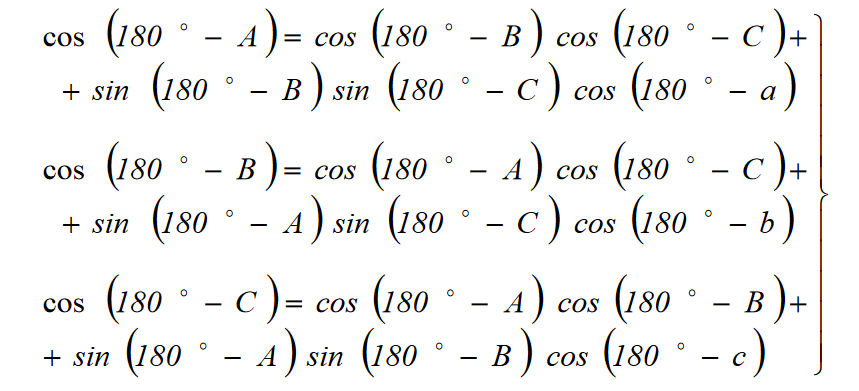
Korzystamy ze wzorów na redukcję funkcji trygonometrycznych

sin(180° − a) = sin(a), cos(180° − A) = -cos(a),

a także pomnóżmy obie części każdego stosunku przez jednostkę ujemną. W rezultacie otrzymujemy wzory na cosinusy kątów trójkąta sferycznego.

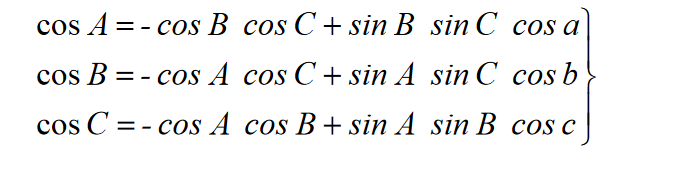
Zatem cosinus kąta trójkąta sferycznego jest równy różnicy między iloczynami sinusów tych samych kątów pomnożonych przez cosinus boku między nimi i cosinusy pozostałych dwóch kątów.

Przykład użycia wzorów: Wyznacz najkrótszą odległość (ortodromię) między A (52°11’; 49°30’) a B(58°17’; 55°36’), które leżą w północnej części kuli ziemskiej (R=6370 km).

Rozwiązanie:

Rozważmy trójkąt sferyczny BPA. Ponieważ CD to łuk równika, P to biegun, a następnie boki ΔBPA są równe AP = 90° - ∠PAO = 90° - φ; BP = 90° - ∠PBO = 90° - φ'.

Różnica długości - kąt ∠BPA = Δλ, równa się λ2 - λ1 = 55°36’ - 49°30’ = 6°06’

Aby określić ortodromię, używamy wzoru na cosinus boku trójkąta sferycznego

cos(a) = cos(b)cos(c)+sin(b)sin(c)*cos A

W naszym przypadku wzór przyjmuje postać:

cos(BA) = cos(90° - φ1)cos(90° - φ2)+sin(90° - φ1)sin(90° - φ2)*cos Δλ
albo:
cos(BA) = sin(φ1)sin(φ2) + cos(φ1)cos(φ2)*cos(Δλ)
Punkt 1
Szerokość φ(1)
Długość λ(1)
Punkt 2
Szerokość φ(2)
Długość λ(2)

§ 3.2 Twierdzenie sinusów

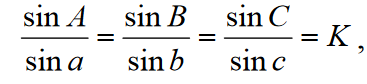TWIERDZENIE: Stosunek sinusa kąta trójkąta sferycznego do sinusa przeciwległego boku jest wartością stałą. Innymi słowy, sinusy boków trójkąta sferycznego są proporcjonalne do sinusów przeciwległych kątów gdzie K = const.

Dowód: W p.3.1 był otrzyman wzór

cos(a) = cos(b)cos(c)+sin(b)sin(c)*cos A

z czego wynika:

Następnie

podzielimy obie części wynikowego wyrażenia przez sin^2(A)

Wyrażenie po prawej stronie równości jest symetryczne względem elementówm (a, b, c) i nie zmieni swojej wartości przy kołowej permutacji liter.

Dlatego K można przyjąć jako stałą i otrzymujemy sin(A)/sin(a) = K

Twierdzenie zostało udowodnione.
    Twierdzenie sinus ustanawia związek między bokami i przeciwległymi kątami trójkąta sferycznego:
  • Równe kąty leżą naprzeciw równych boków trójkąta sferycznego.
  • Największy bok trójkąta sferycznego leży naprzeciw największego kąta i odwrotnie, największy kąt leży naprzeciw największego boku trójkąta sferycznego.
Przykład użycia wzorów: Znane są dwa boki trójkąta sferycznego a = 70°14’; b = 62°10’; i kąt A = 80°20’. Wyznacz kąt B.
Rozwiązanie: Zgodnie z twierdzeniem o sinów dostajemy: sin(B) = sin(A) * sin(B)/sin(a) .

sin(B) = 0,9263

Kąt B = 1,1846rad

§3.3 Wzory na pięć elementów trójkąta sferycznego

    Formuły pięciu elementów ustanawiają związek:
  1. między trzema bokami i dwoma rogami trójkąta sferycznego (podstawowe wzory pięciu elementów);
  2. między trzema kątami i dwoma bokami trójkąta sferycznego (zmodyfikowane wzory pięciu elementów).

Aby otrzymać wzory na pięć elementów, używamy wzoru na cosinusy boków trójkąta sferycznego

Wyeliminuj cos(c) ​​z pierwszego wzoru za pomocą drugiej:

Połączmy wyrazy podobne i podzielmy obie strony równości przez sin(a), otrzymamy:

Jeśli cos(b) jest wykluczone ze wzorów, to przez analogię otrzymujemy

Podobne przekształcenia przeprowadzamy dla pozostałych dwóch par wzorów, otrzymujemy układ wzorów dla pięciu elementów trójkąta sferycznego.

Iloczyn sinusa boku i cosinusa sąsiedniego kąta jest równy iloczynowi sinusa trzeciego boku i cosinusa boku przeciwnego do tego kąta, bez iloczynu cosinusa trzeciego boku i sinus tego samego przeciwległego boku i cosinus kąta między nimi.

Otrzymane wzory są jednorodne pod względem sinusów boków trójkąta sferycznego. Zgodnie z twierdzeniem o sinusach dokonamy zmiany w tych wzorach:

Po prostych przekształceniach otrzymujemy tzw. zmodyfikowane wzory pięciu elementów, które ustalają zależność między trzema kątami i dwoma bokami trójkąta sferycznego.

Iloczyn sinusa kąta razy cosinus sąsiedniego boku jest równy iloczynowi cosinusa kąta przeciwległego do tego boku razy sinus trzeciego kąta plus iloczyn sinusa przeciwnego kąta razy cosinus trzeci kąt i cosinus boku między nimi.

§3.4 Wzory na cztery elementy trójkąta sferycznego

Wybieramy na przykład jedną z formuł z podrozdziału 3.3

Zgodnie z twierdzeniem sinusów

sin(b)*sin(A) = sin(a)*sin(b)

Dzieląc pierwsze równanie przez drugie, otrzymujemy

Tak więc, jeśli po lewej stronie każdej formuły dokonamy zamiany sinusów boków zgodnie ze wzorami uzyskanymi z twierdzeniem sinusów

następnie po prostych przekształceniach otrzymujemy wzory na cztery elementy trójkąta sferycznego:

Jeśli w sferycznym trójkącie, zgodnie ze schematem na rysunku, weźmiemy rząd czterech sąsiednich elementów, na przykład b, C, a, B, wówczas elementy C, a są środkowe, a elementy b, B są skrajny. Wówczas iloczyn cosinusów elementów środkowych jest równy iloczynowi cotangensa skrajnego boku przez sinus środka bez iloczynu cotangensa skrajnego kąta przez sinus kąta środkowego.

§ 3.5 Pytania i ćwiczenia

  1. Jaka jest metoda zamiany?
  2. Ile podstawowych wzorów łączy sześć elementów trójkąta sferycznego?
  3. Jak obliczyć najkrótszą odległość między dwoma punktami na kuli?
  4. Ile podstawowych wzorów łączy pięć elementów trójkąta sferycznego?
  5. Ile podstawowych wzorów łączy cztery elementy trójkąta sferycznego?
  6. Ile niezależnych wzorów z ogólnej liczby wzorów łączących cztery elementy trójkąta sferycznego?
  7. Jaką zależność określa twierdzenie o sinusie sferycznym?